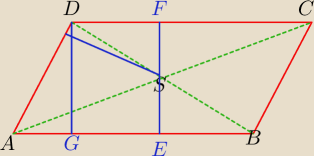
. Piotr 10: Oblicz długości przekątnych równoległoboku o kącie ostrym 30⁰ wiedząc, że odległości punktu przecięcia się przekątnych od prostych zawierających boki równoległoboku są równe 2 i 3. ΔADG

	4
sin300=
	IADI

IADI=8 IABI=y

	1
PΔADS=		*3*8=12
	2

	1
PΔASB=		*2*y=y
	2

	1
PΔADB=		*8*y*sin300
	2

12+y=2y y=12 Z tw. kosinusów (ΔADB)

	√3
IDBI2=82+122 −2*12*8*
	2

IDBI=4√13−6√3 Z tw. kosinusów ( ΔACB)

	√3
IACI2=122+82 −2*8*12*−		=208+96√3
	2

IACI=4√13+6√3 Może ktoś sprawdzić ?

pigor: ..., tak, zgadza się, bo mi wyszło to samo 2 razy z tw. Pitagorasa : AC²= 4²+(12+4√3)²= 16(1+(3+√3)²)= 16(1+12+6√3), stad |AC|=4√13+6√3 i analogicznie dla krótszej przekątnej BD²=4²+(12−4√3)²=...=16(13−−6√3) ⇒ |BD|=4√13−6√3 . ...

Piotr 10: Dziękuję pigor za drugi sposób też , nie wpadłbym na niego

pigor: ..., bo nie próbowałeś go znaleźć, zawsze warto nieco poszukać, aby się nie napracować; pozdrawiam ...

Piotr 10: Wiem, i staram robić się jak umiem zadanie 2 sposobami