. Mariush: Wyznacz rownanie symetralnej poprowadzonej do boku AC A(5;5) B(−1;−3)

Radek: a punkt c ?

Mariush: C(−1;−3) B(−2;4)

Mariush: aucz

Radek: Znajdz wspolczynnik kierunkowy AC, następnie srodek AC i napisz równanie prostej prostopadłej do AC przechodzacej przez środek

Bizon: ... obacz Ty jak trudno przepisać porządnie zadanie ... a co dopiero rozwiązać ... −

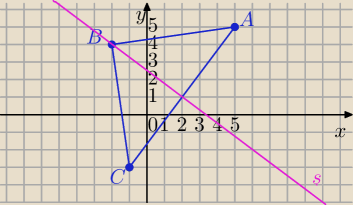
Mila: I sposób Symetralna odcinka AC jest zbiorem wszystkich punktów jednakowo odległych od końców tego odcinka A=(5,5), C=(−1,−3) P(x,y) dowolny punkt symetralnej √(x−5)²+(y−5)²=√(x+1)²+(y+3)² ^2⇔ (x−5)²+(y−5)²=(x+1)²+(y+3)²⇔ x²−10x+25+y²−10y+25=x²+2x+1+y²+6y+9 −10x+50−10y=2x+6y+10 −12x+40=16y /:16

	3		5
s: y=−		x+
	4		2

Mariush: dziekuje Mila