Pazdro. bezendu: Dla jakich wartości parametru p (p∊R) miejsca zerowe x₁,x₂ funkcji kwadratowej f(x)=2x²+(p+3)x+2(p+1)² spełniają warunek x₁x₂(x₁+x₂)<0 ? Δ>0 (p+3)²−4*2*(2p²+4p+2)>0 p²+6p+9−8(2p²+4p+2)>0 p²+6p+9−16p²−32p−16>0 −15p²−26p−7>0/ *(−1) 15p²+26p+7<0 Δ=26²−4*15*7 Δ=256 √Δ=16

	7
p1=−
	5

	1
p2=−
	3

	7		1
p∊(−		,−		)
	5		3

2(p2+2p+1)		−p−3
	*		<0
2		2

(p2+2p+1)(−p−3)
	<0
2

−p3−5p2−7p−3
	<0
2

p³+5p²+7p+3>0 p(−1)=0 (p+1)(−p²−4p−3)>0 (p+1)(p²+4p+3)<0 (p+1)²(p+3)<0 p∊(−∞.−3)∪(−1,∞) Nie wychodzi poprawne rozwiązanie

matyk: A jaka jest odpowiedź?

bezendu:

	6		1
<−		,−1)∪(−1,−		>
	5		3

i jeszcze przedziały domknięte ?

matyk: Domknięte, bo nie masz powiedziane dwa różne miejsca zerowe (to taki mały paradoks). Resztę zaraz sprawdzę

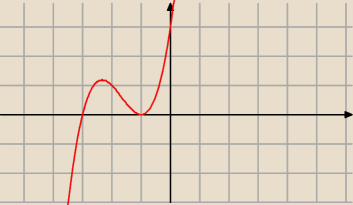
Ajtek: Machnąłeś się w wykresie.

matyk: Masz błąd w nierówności z niej odpowiedź to: p ∊ (−3,−1) ∪ (−1, +∞)

matyk: bezendu my się znamy w ogóle?

bezendu: Rozwiązałem jeszcze raz i wyszła mi nierówność taka jak Tobie, a błąd chyba z tego, że założyłem dwa różne pierwiastki. Dziękuję.

bezendu: @matyk Chyba, że mieszkasz w okolicach Konina. ?

matyk: bezendu ale mi chodzi o np gg i te sprawy

bezendu:

bezendu: W pudełku jest 15 kul w tym co najmniej dwie są żółte a pozostałe czerwone. Jak rozpisać to na drzewku dla dwóch losowań bez zwracania.

bezendu: 2.Jak zapisać liczbę pierwszą ?

Mila: Napisz całe zadanie .

bezendu: W pudełku jest 15 kul w tym co najmniej dwie są żółte a pozostałe czerwone. Ile kul żółtych a ile czerwonych jest w pudełku, jeśli w losowym wyborze dwóch kul z pudełka prawdopodobieństwo

	2
wylosowania dwóch kul żółtych wynosi		?
	35

Chodzi tylko o wytłumaczenie jak to zapisać na drzewku.

bezendu: ?

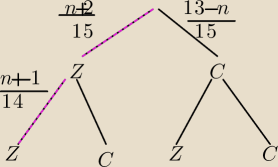
Mila: n+2− liczba kul żółtych 15−n−2=13−n −liczba kul czerwonych

bezendu: Zmyliło mnie to co najmniej. Dziękuję.

bezendu: 4 kule żółte i 11 kul czerwonych.

Mila: Tak.

bezendu: Dane jest równanie x³−(2m+3)x²−5x=0 z niewiadomą x i parametrem m. a) wykaż, że dla każdego m∊R równanie ma trzy pierwiastki, z których dwa mają różne znaki. x[x²−(2m+3)x−5]=0 Δ>0 (2m+3)²+20>0 4m²+12m+29>0 Δ_m=12²−4*4*29 Δ_m=−320 ?

Lorak: Ok, Δ_m ujemna czyli Δ zawsze dodatnia. Trzeba jeszcze dołożyć wzory Viete'a na warunek o różnych znakach i pokazać, że x=0 nie jest rozwiązaniem x²−(2m+3)x−5=0

bezendu: Ok. −5<0 co jest prawdą.

Lorak:

Mila: Δ>0 dla każdego m∊R, zatem równanie x²−(2m+3)x−5=0 ma dwa różne pierwiastki, wykaż, że mają różne znaki. I daj odpowiedź.

bezendu: Iloczyn musi być mniejszy od 0 x₁*x₂<0

−5
	<0
1

−5<0 co jest prawdą ok ?

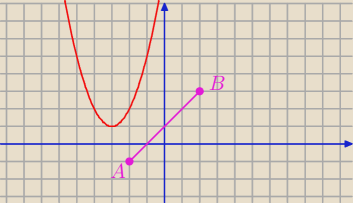
bezendu: Odcinek AB o końcach A(−2,−1) i B=(2,3) jest podstawą trójkąta ABC wierzchołek C należy do wykresu funkcji f(x)=x²+6x+10 wyznacz współrzędne C tak aby pole było najmniejsze. Ile wynosi to pole Co robić dalej ? Wartość najmniejsza jest w wierzchołku

matyk: Jaki jest wzór na pole?

bezendu: Jest w tablicach na trójkąt o podanych 3 wierzchołkach

Lorak: Chodzi o ten najzwyklejszy wzór Pomyśl nad wysokością opuszczoną na odcinek AB

matyk: Można i tak i tak.