Prawdo Radek: Ze zbioru Z = { 1,2,3,...,2n + 1} , gdzie n ∈ N wylosowano równocześnie dwie liczby. Wyznacz n , tak aby prawdopodobieństwo wylosowania liczb, których suma jest liczbą nieparzystą było

	3
większe od
	71

Proszę powiedzieć jak zacząć to ?

	2n+1 2		2n!*2n*(2n+1)
Ω=		=
			2n!*2!

	4n2+2n
Ω=		=2n2+n
	2!

wredulus_pospolitus: nom ... a co z 'A'

Ajtek: |Ω| okej.

Radek: Własnie nie wiem

Ajtek: Kiedy suma dwóch liczb będzie nieparzysta?

Radek: Jeśli dodamy parzystą i nieparzystą.

Ajtek: . Ile w tym zbiorze masz liczb parzystych i nieparzystych?

Radek: 2n+1

Ajtek: Źle się wyraziłem . Ile jest l. parzystych A ile nieparzystych? .

Radek: n parzystych 2n+1 nieparzystych

Radek:

4n2−2n		3
	>
2n2+n		71

?

wredulus_pospolitus: raczej n+1 nieparzystych

Ajtek: Jak uwzględnisz poprawkę wrednego to masz rozwiązanie.

Radek:

2n2+3n+1		3
	>
2n2+n		71

Ajtek: Skąd wziął się licznik?

Radek: parzyste powinno być chyba 2n a nieparzyste 2n+1 bo jeśli będę miał n+1 to podsawiajac za n=1 mam 2 a to jest parzyste.

Ajtek: n parzystych i n+1 nieparzystych n+n+1=2n+1 czyż nie .

Radek: ale liczbę parzystą zapisujemy 2n przecież ?

Radek: ?

Radek: ?

Ajtek: Nie chodzi mi o zapisanie liczby parzystej. Masz 2n+1 liczb. Ilość parzystych wynosi n, zaś nieparzystych n+1

wredulus_pospolitus: Radek ... masz 2n+1 liczba ile z nich to będa liczby nieparzyste a ile z nich to będa liczby parzyste

Radek: n parzystych i n+1 nieparzystych albo na odwrót ?

Mila: 1,2,3,4,5,6,7,8,9 masz 9 liczb 4 parzyste 5 nieparzystych 2n+1=9 2n=8 n=4 1,2,3,4,5,6,7.....,2n+1 n− liczba parzystych n+1 − liczba nieparzystych, co razem daje: n+n+1=2n+1

Radek: A może być ten drugi zapis ?

Ajtek: Witaj Mila . Przypilnujesz, ja muszę do apteki migiem lecieć. Będę za jakieś pół godziny .

Radek: Może być, że parzystych jest n+1 a nieparzystych n ?

wredulus_pospolitus: nie .... nie może być ponieważ ... masz 2n+1 liczb ... pierwszą (najmniejszą liczbą) będzie na pewno '1' i jest to liczba nieparzysta ... najwiekszą liczbą będzie 2n+1 ... która także NAPEWNO jest nieparzysta

Radek: W urnie znajdują się jedynie kule białe i czarne. Kul białych jest trzy razy więcej niż czarnych. Oblicz, ile jest kul w urnie, jeśli przy jednoczesnym losowaniu dwóch kul

	9
prawdopodobieństwo otrzymania kul o różnych kolorach jest większe od
	22

Tak będzie wyglądało drzewko ?

Mila: Trzeba jeszcze napisać co było losowane B lub C. Oblicz, ile jest tych kul.

Radek: Za chwilkę wstawię.

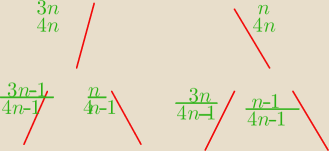
Radek:

3n		n		n		3n		9
	*		+		*		>		?
4n		4n−1		4n		4n−1		22

Ok?

Mila: Tak, teraz uprościć przez n.

Radek: 4 albo 8 kul ?

Mila: Zgadza się .

Radek: Mogę jeszcze prosić o pomoc w diagramach venn'a ?

Mila: Tak.

Radek:

	1		1
Dane są dwa takie zdarzenia A i B , że P(B)≤		i P (A ∩ B )≥		Czy może zachodzić
	3		10

	4
równość P(B∖A)=		? Odpowiedź uzasadnij.
	15

wredulus_pospolitus: Wybierzmy najbardziej 'pożądaną' sytuację:

	1		5
P(B) =		=
	3		15

	1
P (A ∩ B ) =
	10

	1		1		5		1		4
P(B∖A) = P(B) − P (A ∩ B ) =		−		<		−		=
	3		10		15		15		15

Odp: Nie ma takiej możliwości.

Mila:

	1		1
P(B\A)=P(B)−P(A∩B)≤		−P(A∩B) zwiększyłam odjemną, teraz odejmę
	3		10

	1		1		10−3		7		4		8
≤		−		=		=		<		=
	3		10		30		30		15		30

Odp. Nie może zachodzić równość:

	4
P(B\A)=
	15

Radek: A tego też nie robię się na diagramach ?

wredulus_pospolitus: a po co ?

Radek: Żeby lepiej zrozumieć ?