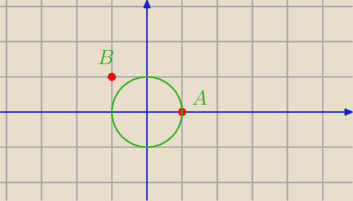
ge RS: Dane są punkty A (1,0),B(− 1,1) . Punkt C należy do okręgu o równaniu x²+y²=1.Znajdź współrzędne punktu C , tak aby pole trójkąta było największe. Oblicz to pole. O co tutaj chodzi ?

wredulus_pospolitus: chodzi o znalezienie punktu C takiego aby pole było jak największe procedura jest prosta wyznaczasz odcinek AB (podstawa trójkąta) wyznaczasz prostopadłą do odcinka AB (pokazuje 'kierunek' wysokości trójkąta) pole trójkąta zależy od: podstawy (która jest stała bo jest to odcinek AB) i wysokości Wiec im większa wysokość tym większe pole znajdź zatem takie ustawienie prostej prostopadłej do AB, aby wysokość była największa

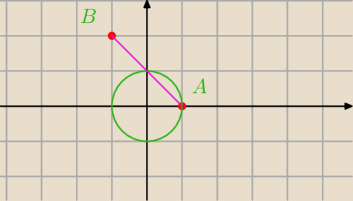
RS: |AB|=2 y=2x+b prostopadła do odcinka AB Ale nie wiadomo jaki to trójkąt więc wysokość nie musi padać na połowę podstawy przecież ?

wredulus_pospolitus: dlaczego punkt B z (−1,1) powędrował na (−1,2)

wredulus_pospolitus: RS ... to inaczej ... tworzysz prostą równoległą do odcinka AB ... sprawdzasz dla jakiego punktu (okręgu) prosta o takim współczynniku kierunkowym będzie styczną do tegoż okręgu ... wyjdą Ci dwa punkty ... (jeden w III ćwiartce −−− tego szukasz ... a drugi w I ćwiartce)

RS: A możesz odpowiedzieć na moje pytanie z 16:57 ?

wredulus_pospolitus: a czy ja gdziekolwiek napisałem że ma padac na polowę oczywiście, że nie wiadomo jaki to będzie trójkąt ... a więc na kartce byś linijką 'przesuwał' się od punktu A do punktu B ... patrząc gdzie 'odległość' będzie największa

wredulus_pospolitus: a nawet dalej niż tylko od A ... ale to już inna para kaloszy

RS: A mógłbyś mi pokazać jak znaleźć algebraicznie tę prostą prostopadła y=2x+b ?

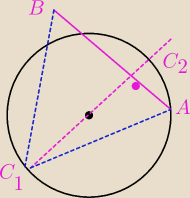
Mila: Część odcinka AB jest cięciwą okręgu, najdłuższy odcinek prostopadły do cięciwy przechodzi przez środek okręgu, tutaj przez punkt(0,0).

	1		1
AB: y=−		x+
	2		2

m⊥AB: y=2x Teraz szukaj punktu C przecięcia z okręgiem i oblicz |h| x²+(2x)²=1

RS: Muszę pomyśleć.

RS: Nie rozumiem czemu tutaj akurat skorzystano z cięciwy. ?

Mila: AB przecina okrąg.

RS: To chyba nie dla mnie.

RS: Ale za rozwiązanie dziękuję.

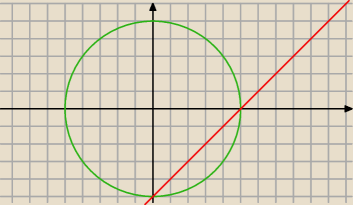
RS: Ostrokątny trójkąt równoramienny ABC o podstawie AB jest wpisany w okrąg o równaniu x²+y² = 25 . Punkty A i B leżą na prostej o równaniu y=x−5 Współrzędne punktów AB z przecięcia się prostej z okręgiem a C z wysokość z okręgiem ?

5-latek: Punkty A i B to punkty przeciecia prostej z okregiem A co masz obliczyc ?

bezendu: Jeden będzie tylko punkt C bo drugi nie będzie spełniał warunków zadania.