Fizyczne Marcin: Poszukać środka ciężkości stożka. Wiem, że stożek trzeba postawić wierzchołkiem do dołu i podzielić go na warstwy o grubości dy i

	r		R
promieniu r. Z podobieństwa trójkątów wynika, że:		=
	y		H

Może mi ktoś wytłumaczyć skąd się bierze pozniej równanie: dm=πr²ρdy

wredulus_pospolitus: a co to jest dm

Marcin: widziałem gdzieś na necie takie równanie do tego zadania i próbuję go rozkminić.... masz może inny pomysł na to zadanie?

wredulus_pospolitus: eeee zacznijmy od tego ... że zrobisz to w prosty sposób

wredulus_pospolitus: a nie jakies tam całki i inne różniczki

Marcin: chyba bardziej powinno się wykorzystać ten wzór http://pl.wikipedia.org/wiki/%C5%9Arodek_masy

Marcin: No ale chyba to będzie mniej dokładne, czy nie?

wredulus_pospolitus: nie ,,, nie trzeba zauważ, że jest to środek ciężkości ukladu w ruchu ... a stożek nie jest w ruchu

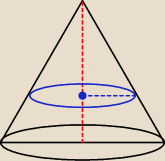
wredulus_pospolitus: oczywiście ... środek ciężkości będzie leżał gdzieś na wysokości stożka (symetria przede wszystkim) Twoim zadaniem jest znalezienie w jakiej odległości od 'czubka' będzie się ów punkt znajdował h −−− wysokość małego stożka (czyli odległość środka ciężkości od 'czubka' stożka)

	1
Vm =		πr2*h
	3

	1
VM =		πR2*H
	3

iii ma zachodzić: V_M = 2*V_m

	h		H		H
z tw. Talesa (podstawówka/gimnazjum) wiesz, że		=		−> h =		*r
	r		R		R

czyli:

	1		2		H		2
VM =		πR2*H =		πr2*		*r =		πr2*h = 2*Vm
	3		3		R		3

a stąd masz: R³ = 2r³

	R3√4
r =
	2

	H3√4
... a więc h =
	2