g
Radek:
Wyznacz współrzędne wierzchołków trójkąta jeżeli środki jego boków mają współrzędne: P =
(1,3),Q = (− 5,4),R = (− 6,7)
Wiem, że robi się układ ale jak ?
10 sty 15:21
wredulus_pospolitus:
A = (x
a,y
a)
B = (x
b,y
b)
C = (x
c,y
c)
niech P będzie środkiem odcinka: AB
w takim razie: (x
b−x
a ; y
b − y
a) = (1 ; 3) <−−− dwa równania
analogicznie pozostałe punkty
i masz 6 równań z sześcioma niewiadomymi

... powodzenia
10 sty 15:25
Radek:
A czy ta kolejność jest ważna ?
10 sty 15:31
Radek:
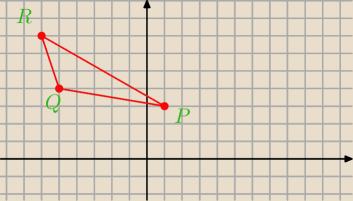
P=(x
a,y
a)
Q=(x
b,y
b)
R=(x
c,y
c)
co mam wpisać zamiast ?
10 sty 15:35
wredulus_pospolitus:
nie jest istotna ... najwyżej punkt A nie będzie w 'lewym dolnym wierzchołkiem' trójkąta

10 sty 15:39
wredulus_pospolitus:
jak to się zwykło zaznaczać
10 sty 15:39
Radek:
Q(x
a,y
a)
P=(x
b,y
b)
R=(x
c y
c)
| xa+xb | | xa+xb | |
| =−5 czy |
| =1 |
| 2 | | 2 | |
10 sty 15:43
10 sty 15:45
wredulus_pospolitus:
yyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyy
yyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyy
yyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyy
dlaczego:
Q(x
a,y
a)
P=(x
b,y
b)
R=(x
c y
c)
i w jakim celu

10 sty 15:46
Radek:
Żeby punkt A był lewym dolnym wierzchołkiem tak jak zwykło się oznaczać.
10 sty 15:47
wredulus_pospolitus:
a co za różnica który będzie punkt A

natomiast oznaczenie jako Q = (x
a,y
a) nie ma absolutnie żadnego sensu ... zmazuj to
i zastanów się jeszcze raz
| xa+xb | |
| = xśrodka odcinka AB |
| 2 | |
jeżeli chcesz punkt A, aby był jako lewy dolny narożnik ... to x
środka odcinka AB = x
Q
analogicznie: x
środka odcinka AC = x
R oraz x
środka odcinka BC = x
P
10 sty 15:51
kika:
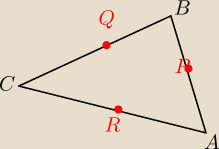
10 sty 15:51
Radek:
Dziękuję teraz już chyba sobie poradzę.
10 sty 15:53
PW: Wiadomo, że prosta PR jest równoległa do prostej BC. Wystarczy więc napisać równanie prostej
PR, a następnie równanie równoległej do niej przechodzącej przez Q − otrzymamy równanie
prostej BC. Powtórzyć to samo dla prostej PQ i równoległej do niej AC oraz dla prostej QR i
równoległej do niej AB. Mając równania trzech boków rozwiązać trzy układy równań − dla każdej
pary uzyskamy jeden wierzchołek trójkąta.
Inna koncepcja to wykorzystanie faktu, że trójkąty PQR i CAB są jednokładne, stosunek
jednokładności k=−2. Gdyby umiał znaleźć środek jednokładności S, to odpowiedź byłaby
natychmiastowa − A jest obrazem Q, B jest obrazem R i C jest obrazem P w jednokładności o
środku S i stosunku −2.
10 sty 16:24
 ... powodzenia
... powodzenia
 P=(xa,ya)
Q=(xb,yb)
R=(xc,yc)
P=(xa,ya)
Q=(xb,yb)
R=(xc,yc)





 natomiast oznaczenie jako Q = (xa,ya) nie ma absolutnie żadnego sensu ... zmazuj to
i zastanów się jeszcze raz
natomiast oznaczenie jako Q = (xa,ya) nie ma absolutnie żadnego sensu ... zmazuj to
i zastanów się jeszcze raz
