Wzór
Daras: P(A' ∩ B) − jak to obliczyć?
10 sty 13:51
wredulus_pospolitus:
najprościej jak się da

10 sty 14:05
wredulus_pospolitus:
albo jak wolisz to:
szybko i sprawnie

a najlepiej to: bezbłędnie

10 sty 14:05
Daras: Haha, tyle, to ja wiem.

A poratuje ktoś wzorem?
10 sty 14:08
wredulus_pospolitus:
nie ma 'jakiegoś wzoru' wszystko zależy od tego jakie masz dane ... stąd też takie a nie inne
moje odpowiedzi
10 sty 14:29
Daras: | | 2 | | 3 | | 3 | |
Mam podane P(A) które wynosi |
| , P(B) = |
| P(A∪B) = |
| , |
| | 5 | | 10 | | 5 | |
| | 3 | | 1 | |
wyliczyłem P(A') = |
| i P(A ∩ B) = |
| . |
| | 5 | | 10 | |
Zostało mi do wyliczenia już tylko P(A' ∩ B) i nie bardzo wiem, jak się za to zabrać.
10 sty 14:36
wredulus_pospolitus:
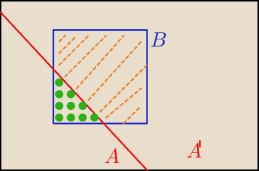
no i widzisz ... teraz juz wiemy na czym możemy 'pracować'
zauważmy, że P(A') = 1−P(A)
ale także: P(A' ∩ B) = P(B) − P(A ∩ B)
najlepiej to na rysunku zauważyć:
10 sty 14:42
kika:
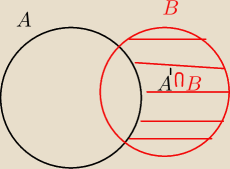
10 sty 14:46
wredulus_pospolitus:
Możesz to też wyliczyć w następujący sposób:
P(A'uB) = P(A') + P(B) − P(A' ∩ B)
szukamy : P(A'uB)
zauważmy, że: P(A'uB) = P(A') + P(A∩B) = 1 − P(A) + P(A∩B)
10 sty 14:46
wredulus_pospolitus:
słownie:
P(A'uB) = zbiór A' + ta część zbioru 'B' które NIE MA części wspólnej ze zbiorem A'
10 sty 14:47
wredulus_pospolitus:
czyli ostatecznie to będzie:
P(AuB) − P(A) = P(A'∩B)

10 sty 14:49
Daras: Dzięki wielkie. <3333
10 sty 14:54

 a najlepiej to: bezbłędnie
a najlepiej to: bezbłędnie 
 A poratuje ktoś wzorem?
A poratuje ktoś wzorem?
 no i widzisz ... teraz juz wiemy na czym możemy 'pracować'
zauważmy, że P(A') = 1−P(A)
ale także: P(A' ∩ B) = P(B) − P(A ∩ B)
najlepiej to na rysunku zauważyć:
no i widzisz ... teraz juz wiemy na czym możemy 'pracować'
zauważmy, że P(A') = 1−P(A)
ale także: P(A' ∩ B) = P(B) − P(A ∩ B)
najlepiej to na rysunku zauważyć:

