ge
RS:
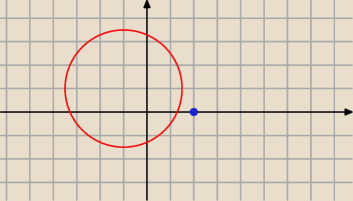
Znajdź równania stycznych do okręgu (x+1)
2+(y−1)
2=5 poprowadzonych z punktu A = (2,0)
Wskazówki
9 sty 19:27
MQ: pęk prostych w pk. A ma postać: y=a(x−2)
Podstawiasz to do równania okręgu i szukasz rozwiązań, które dają jeden pierwiastek, czyli Δ=0.
Powinieneś dostać dwa rozwiązania −− dwie wartości a.
9 sty 19:31
RS:
Nie bardzo rozumiem. pęk prostych ?
9 sty 20:48
MQ: No, wiązka.
9 sty 20:49
RS:
Ale nadal nie rozumiem ?
9 sty 20:51
MQ:
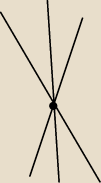
To jest pęk (wiązka) prostych −− przechodzi ich przez ten punkt nieskończenie wiele.
9 sty 20:54
RS:
MQ wiem, że pęk ale jak wyznaczyć te proste ?
9 sty 20:55
MQ: No przecierz ci napisałem!
Podstawiasz y do równania okręgu −− dostajesz równanie kwadratowe na x.
Punkt styczny, to rozwiązanie, gdy masz tylko jeden pierwiastek, czyli Δ=0
Ta Δ będzie zależna od a, więc szukasz takich a, żeby Δ=0.
Dostaniesz dwa rozwiązania −− dwie wartości a.
9 sty 20:58
5-latek: Z Twojego rysunku widac ze beda dwie takie proste styczne do tego okregu
jak napisal MQ przez punkt A mozemy poprowadzic pek prostych
Ale prosta o rownaniu x=2 nie jest zadna z szukanych stycznych wic zajmujemy sie dalej
rodzina prostych y=a(x−2) i a nalezy do R wsrod ktorych znajdzuja sie obie szukane styczne
.
wobec tego na taki uklad rownann
{(x+1)2+(y−1)2=5
{y=a(x−2) musisz nalozyc warunek ze delta =0
Wiec wylicz a i naoisz rownania tych stycznych
9 sty 21:11
Mila:
Łatwiej Ci będzie skorzystać, że odległość S(−1,1) od prostej stycznej y=ax−2a jest równa
√5
y=ax−2a [prosta przechodząca przez punkt (2,0) ]
ax−y−2a=0 postać ogólna tej stycznej.
| | |ax−y−2a| | |
d= |
| =√2 za x i y podstaw wsp punktu S. |
| | √a2+1 | |
9 sty 21:27
Mila:
√5 zamiast √2, pomyliłam klawisze.
9 sty 21:28
RS:
Dziękuję zaraz będę rozwiązywał
9 sty 21:34
9 sty 21:41
MQ: Wygląda dobrze, ale bardziej elegancko wyglądałoby tak:
y=−2(x−2)

9 sty 21:49
RS:
Dziękuję.
9 sty 21:51
Mila:
Dobrze.
9 sty 21:54
RS:
Mogę jeszcze prosić o pomoc ?
9 sty 21:54
RS:
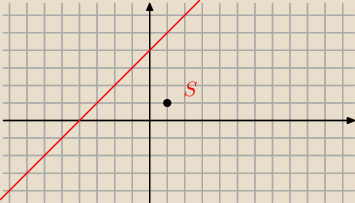
Napisz równanie okręgu o środku S(1,1) , który na prostej o równaniu x−y+4=0 odcina cięciwę AB
długości 2
√2 . Wykonaj rysunek
?
9 sty 22:13
RS: ?
9 sty 22:18
Eta:
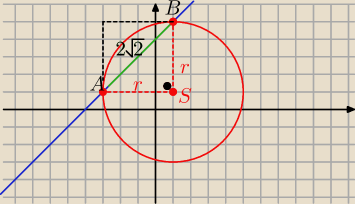
r=........
9 sty 22:22
RS:
r=2
9 sty 22:24
MQ: Ja bym to zrobił tak:
Całe rozwiązanie zależne jest od promienia okręgu r.
Równanie okręgu:
(x−1)2+(y−1)2=r2
1. podstawiam, y=x−4 do równania.
2. dostaję r. kwadratowe na x z współczynnikami zależnymi od r.
3. liczę pierwiastki −− dostanę 2 na wsp. x (przy odpowiednim warunku na Δ.
4. liczę wsp. y dla x−ów.
5. liczę odległość jako pierwiastek z (x1−x2)2+(y1−y2)2
6. jest ona zależna od r
7. przyrównuję ją do 2√2 −− wyliczam r
9 sty 22:24
RS:
Dziękuję za rysunek i schemat do zadania.
9 sty 22:25
Eta:
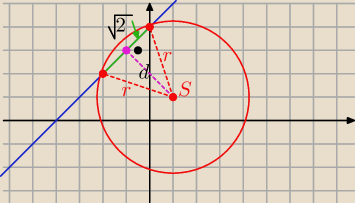
Echh .. niestety ale źle narysowałam ( z rys. to r= 4 , a to nie jest prawdą, bo wtedy
długość cięciwy byłaby = 4
√2
no to poprawiam :
1 / oblicz odległość "d" środka S od tej prostej
2 / z tw. Pitagorasa r
2= d
2+(
√2)
2 =...
3/ o: .........
Przepraszam za wprowadzenie w błąd

9 sty 22:41
MQ: Tak to jest włąśnie, jak miesza się planimetrię z geometrią analityczną

9 sty 22:42
RS:
Właśnie ta cięciwa może być różnie rozmieszczona skąd wiadomo, że akurat w tym miejscu ?
9 sty 22:42
RS: ?
9 sty 22:48
MQ: Bo takie jest równanie prostej
9 sty 22:50
 Znajdź równania stycznych do okręgu (x+1)2+(y−1)2=5 poprowadzonych z punktu A = (2,0)
Wskazówki
Znajdź równania stycznych do okręgu (x+1)2+(y−1)2=5 poprowadzonych z punktu A = (2,0)
Wskazówki
 To jest pęk (wiązka) prostych −− przechodzi ich przez ten punkt nieskończenie wiele.
To jest pęk (wiązka) prostych −− przechodzi ich przez ten punkt nieskończenie wiele.

 Napisz równanie okręgu o środku S(1,1) , który na prostej o równaniu x−y+4=0 odcina cięciwę AB
długości 2√2 . Wykonaj rysunek
?
Napisz równanie okręgu o środku S(1,1) , który na prostej o równaniu x−y+4=0 odcina cięciwę AB
długości 2√2 . Wykonaj rysunek
?
 r=........
r=........
 Echh .. niestety ale źle narysowałam ( z rys. to r= 4 , a to nie jest prawdą, bo wtedy
długość cięciwy byłaby = 4√2
no to poprawiam :
1 / oblicz odległość "d" środka S od tej prostej
2 / z tw. Pitagorasa r2= d2+(√2)2 =...
3/ o: .........
Przepraszam za wprowadzenie w błąd
Echh .. niestety ale źle narysowałam ( z rys. to r= 4 , a to nie jest prawdą, bo wtedy
długość cięciwy byłaby = 4√2
no to poprawiam :
1 / oblicz odległość "d" środka S od tej prostej
2 / z tw. Pitagorasa r2= d2+(√2)2 =...
3/ o: .........
Przepraszam za wprowadzenie w błąd 
