g RS: Dany jest okrąg o równaniu x²+y²−10x+4y+25=0 . Napisz równania stycznych do tego okręgu, przechodzących przez początek układu współrzędnych x²+y²−10x+4y+25=0 (x−5)²−25+(y+2)²−4+25=0 (x−5)²+(y+2)²=4 S=(5,−2) r=2 Dalej proszę o wskazówki a nie pisanie gotowców.

Eta:

Piotr 10: Jeżeli prosta przechodzi przez początek układu współrzędnych jest postaci y=ax

Saizou : napiszę jeden znak i 2 literki r=d wystarczająca podpowiedź

Eta: Hej Saizou ...

Saizou : cześć Eto i Piotrze

Basia: prosta przechodząca przez początek układu ma równanie y = ax lub x=0 sposób 1 badasz ile rozwiązań ma układ: x = 0 x²+y²−10x+4y+25=0 jeżeli jedno to prosta x=0 (czyli oś OY) jest jedną z szukanych stycznych badasz dla jakiej wartości parametru a układ y = ax x²+y²−10x+4y+25=0 ma dokładnie jedno rozwiązanie sposób 2 badasz jaka jest odległość prostej x=0 od S jeżeli = r (czyli 2) to ta prosta jest styczną badasz dla jakiej wartości parametru a odległość S od prostej ax−y=0 jest równa r

RS: ? wiem, że prosta przechodząca przez (0,0) ma równanie y=ax ale dalej nie kumam.

RS: ?

Basia: niekoniecznie; oś OY przechodzi przez punkt (0,0) i nie ma równania postaci y=ax, bo nie jest wykresem funkcji dlatego oprócz równania y=ax rozpatrujesz też równanie x=0 prosta jest styczna do okręgu ⇔ ma z nim dokładnie jeden punkt wspólny ⇔ układ równań {równanie prostej} i {równanie okręgu} ma dokładnie jedno rozwiązanie albo prosta jest styczna do okręgu ⇔ odległość środka okręgu od tej prostej = promieniowi okręgu

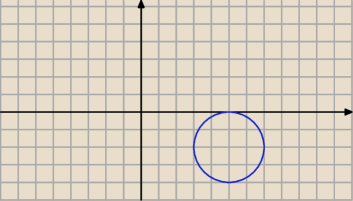
RS: zgodnie z drugim sposobem jedna styczna to x=0 jak wyznaczyć drugą ?

Basia: to jest prosta y=0 (oś Ox) a nie x=0 prosta x=0 nie jest styczna do tego okręgu, bo układ x = 0 x²+y²−10x+4y+25=0 y²+4y+25=0 nie ma rozwiązania; Δ<0 y = ax x²+y²−10x+4y+25=0 x² + (ax)² − 10x + 4*(ax)+25 = 0 (1+a²)x² + (4a−10)x + 25 = 0 Δ = (4a−10)² − 4(1+a²)*25 i ma być jedno rozwiązanie czyli (4a−10)² − 4(1+a²)*25 = 0 dalej potrafisz rozwiązać ?

RS: Tak potrafię, mam jeszcze pytanie ? Który sposób jest bardziej praktyczny ?

Basia: oba prowadzą do takiego samego równania, co możesz spróbować sprawdzić

RS: Ale z pierwszego wychodziło mi równanie sprzeczne i wybrałem drugi sposób, Dziękuję.