; Radek: Diagramy Venn'a

	1		1		1
Oblicz prawdopodobieństwo P(A'∩B') jeżeli P(A')=		P(B')=		P(A∩B)=
	3		4		2

P(A'∩B')=P(A)+P(B)−P(A∩B)

	11
P(A'∩B')=
	12

Godzio: P(A'∩B') = P(A') + P(B') − P(A'UB') = P(A') + P(B') − (1 − P(A∩B) ) =

	1		1		1		1
=		+		− (1 −		) =
	3		4		2		12

matyk: Niestety, ale nie

matyk: Znaczy się Godzio masz ok Radek ma źle

Radek: P(A')=P(B)−P(A∩B) P(B')=P(A)−P(A∩B) Idąc tym tropem tak napisałem dlaczego źle ?

Mila: Radek Możesz skorzystać z prawa de Morgana. (A∩B)'=A'UB'

	1		1
P((A∩B)')=P(A'UB')=1−P(A∩B)=1−		=
	2		2

Wtedy korzystasz ze znanego wzoru na prawd. sumy zbiorów. P(A'UB')=P(A')+P(B')−P(A'∩B')

1		1		1
	=		+		−P(A'∩B')
2		3		4

6		4		3
	=		+		−P(A'∩B')
12		12		12

	1
P(A'∩B') =
	12

Radek: Ale czemu mój tok rozumowani jest błędny ?

Godzio: P(A') = P(B) − P(A∩B) ⇔ 1 − P(A) = P(B) − P(A∩B) ⇔ P(A∩B) = P(A) + P(B) − 1 A to nie musi być prawdą bo nie wiemy czy P(A U B) = 1, więc zły wzór wykombinowałeś

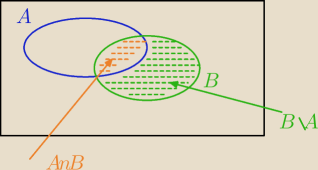
Mila: Ponadto : P(B)−P(A∩B)=P(B\A)

Radek: Jeszcze mam takie pytanie lepiej robić arkusze czy konkretne zadnia z zadani,info ?

Godzio: Do rozszerzenia i arkusze i zadania.info, chodzi o ćwiczenie trudnych zadań, rozszerzenie się raczej nie powtarza, więc to nie ma wpływu skąd robisz

Radek: Dzięki