Równoległobok o bokach a=16 b=10 matematyka: Równoległobok o bokach a=16 b=10 oraz kącie ostrym α=60* obracamy dookoła krótszego boku. Oblicz objętość i pole powierzchni całkowitej bryły.

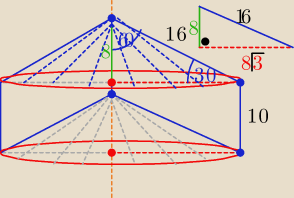
Eta: Powstała bryła jest walcem z wydrążonym stożkiem od dolnej podstawy walca i jednocześnie naklejonym stożkiem( o tych samych wymiarach) na górną podstawę walca zatem: V(bryły)= V(walca) (to tak jakbyśmy odcięli górny stożek i włożyli go w "lukę" w dolnej podstawie walca ( więc objętość bryły będzie równa V(walca P_c(bryły)= 2P_b(stożków +P_b (walca) Pole całkowite , to tak jakbyśmy mieli pomalować taką bryłę farbą czyli malujemy dwie powierzchnie boczne stożków i powierzchnię boczną walca Mam nadzieję,że to rozumiesz Wymiary walca : H_w= b=10 , r_w= r_st= h_b (równoległoboku)= 8√3 Wymiary stożka : H_st= 8 , l_st= a= 16 Podstaw dane i dokończ obliczenia........

Eta: A może do tej pory ....... masz już rozwiązane samodzielnie