Trygo Kostek: Rozwiąż równanie 2sin²x+sinx−1=0 2sin²x+sinx=1 sinx(2sinx+1)=1 sinx=1 lub 2sinx+1=1 Tak czy nie ?

Ajtek: Nie W tego typu przypadkach zawsze wchodzisz w równanie kwadratowe

Kostek: sinx=u u∊<−1,1>

Ajtek: Dokładnie tak .

Eta: 2sin²x +sinx−1= (2sinx−1)(sinx+1) =0 i teraz działaj .........

Ajtek: Co expert, to expert. Łap Eta .

Eta:

Ajtek: Eta masz pigwó.....

Kostek: 2sinx=1

	1
sinx=		lub sinx=−1
	2

	π		5π
x=		+2kπ lub x=		+2kπ
	6		6

	π		π
x=−		+2kπ x=		+2kπ
	2		2

Ajtek:

	π
sinx=−1 dla x=
	2

Eta: https://matematykaszkolna.pl/strona/1571.html zobacz sinx= −1

Kostek:

3π
	czyli 4 rozwiązania ?
2

Marcin:

	3
sin = −1 dla x=		π + 2kπ
	2

Kostek:

	π
sinx=−1 dla x=−
	2

Kostek: ?

Eta:

	π		π		3
−		= 2π−		= +		π
	2		2		2

Kostek: 2π ? Przeca odejmujemy od π ?

ZKS: Można zapisać tę odpowiedź jako

	π		π		2
x = −		+ k * 2π ∨ x =		+ k *		π.
	2		6		3

O ile się nie mylę.

Kostek: sinx+cos²x+1=0 sinx+cos²+sin²x+cos²x=0 sinx+sin²x+2cos²x=0 ?

Kostek: ?

Ajtek: Ależ Ty kombinujesz cos²x=1−sin²x Cześć ukrywający sie .

Marcin:

	π		3
Można zapisać i tak i tak, ale przecież −		+ 2kπ =		π
	2		2

Ajtek: Marcin nigdy w życiu

	1		3
Czy −		+2x=		dla x∊Z
	2		2

Kostek: Ale ja nadal nie rozumiem czemu tak a nie tak jak ja podałem ?

Ajtek: Kostek szukasz f. jednej zmiennej. Albo sinx albo cosx.

Kostek: Nie o to chodzi. 23:34 ?

Ajtek: Okres funkcji sinx wynosi 2π. Co π się tylko zeruje .

Kostek: To czemu mój zapis nie jest poprawny ?

Marcin: Ajtku, ale jeżeli za k podstawimy 1, to to co napisałem będzie prawdą, tak?

Ajtek: Zapis z 23:25

Ajtek: Ale tylko dla k=1 .

ZKS: Witam Ajtek i wszystkich tutaj zebranych. Można też zrobić w taki sposób 2sin²(x) + sin(x) − 1 = 0 −[1 − 2sin²(x)] + sin(x) = 0 −cos(2x) + sin(x) = 0 cos(2x) = sin(x)

	π
cos(2x) = cos(		− x).
	2

Kostek:

Marcin: A więc jeżeli sin lub cos = 1 lub −1, to wystarczy jedno rozwiązanie, ale jeżeli sin lub cos jest pomiędzy jedynkami, to rozwiązania mają być dwa.

Ajtek: ZKS teraz to dowaliłeś Łap w nagrodę. http://www.youtube.com/watch?v=hJwN9nISv00

ZKS: To masz i również ode mnie. http://www.youtube.com/watch?v=0uepMnz3-9U

ZKS: Marcin nie ma czegoś takiego jak cos = 1 ale cos(x) = 1 już tak (bądź inny argument). Taka malutka uwaga.

Eta: http://pl.wikipedia.org/wiki/K%C4%85t_skierowany Można też odświeżyć wiedzę o kątach skierowanych wtedy wszystko się wyjaśni

Kostek: Nie rozjaśniło się ?

Kostek: ?

Marcin: sinx+cos2x+1=0 ⇔ −sinx² + sinx + 2 = 0 Δ = 9 ⇔ √Δ = 3

	−1−3
x1 =		⇔ 2 Nie należy
	−2

	−1+3
x2 =		⇔ −1
	−2

sinx= −1

	3
x=		π + 2kπ
	2

będzie dobrze?

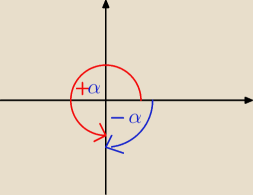
Eta: −90^o= +270^o= 360^o−90^o zatem

	π		π		3
−		= 2π−		=		π
	2		2		2

Kostek:

	π
ale czemu nie może zostać to −		?
	2

Eta: Może zostać bo to jest taka sama odpowiedź , tylko kąt jest ujemny! Miłych snów

Marcin:

	7
równie dobrą odpowiedzią będzie		π
	2

Kostek: Dziękuję i dobranoc. wrócę jutro.