Trygo Kostek: Trochę mnie tu nie było i wracam z tym samym problemem. A mianowicie trygonometria. Wytłumaczy ktoś równania trygonometryczne w przedziale ?

Kostek: Proszę wytłumaczcie mi to krok po kroku. rozwiąż równanie 2sin²x+3cosx=0 w przedziale <0,2π>

Trivial: Skorzystaj z sin²x = 1−cos²x, a potem podstaw u = cosx, u∊[−1,1] i rozwiązuj dalej.

Ajtek: A gdyby nie było przedziału to wiesz jak to rozwiązać

Kostek: A nie da rady bez podstawienia ?

Ajtek: Z podstawieniem łatwiej .

Kostek: A jak rozwiązać bez przedziału ?

Ajtek: Tak jak napisał Trivial .

Kostek: Nic. proste równania z tej strony potrafię zrobić ale rozbudowane to Amen a we wtorek próbna matura.

Ajtek: 2(1−cos²x)+3cosx=0 −2cos²x+3cosx+2=0 u=cosx i −1≤u≤1 2u²−2u−2=0 Wiesz co dalej?

Kostek: 2(u²−u+1)=0 Δ?

Ajtek: Sorry błąd 2u²−3u−2=0

Kostek: teraz Δ. Δ=25

	1
u1=−
	2

u₂=2

Ajtek: Wracasz do podstawienia. −1≤u≤1 Jak widzisz u₂ odpada, dlaczego

Piotr 10: W przyszły wtorek próbna matura z OKE z matematyki poziom rozszerzony,tak ?

Kostek: Tak. Na próbnej miałem 70 to dostałem zj... bo trygonometrii nie ruszyłem.

Kostek: Ajtek cos<−1,1>

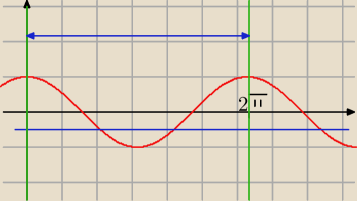
Ajtek: No to masz teraz: cosx=−0,5 Odczytaj teraz z wykresu te wartości kąta, dla których cosx=−0,5 Interesuje Ciebie tylko to co jest pomiędzy zielonymi liniami. Tylko te rozwiązania.

Kostek: Ok dzięki zaraz wstawię kilka do sprawdzenia

Ajtek: O stary, do czego Ty mnie zmuszasz .

Kostek: Nie zmuszam Cię do niczego. I taki stary nie jestem bo mam naście lat jeszcze.

Ajtek: Z tym starym to wiesz o co chodzi. Mam taką nadzieję . Zmuszać nie zmuszasz, ale nie chce mi się liczyć tego wszystkiego. Ale wrzuć może coś poradzimy .