. Piotr 10: Dany jest ciąg funkcji f_n(x)= −3x²+(n−6)*x+5. Określ ciąg (w_n) największych wartości tych funkcji. Sporządź jego wykres dla n ≤ 12 i podaj zbiór wartości. Mogę prosić o wskazówkę ?

Mila: x_w(n) y_w(n)

Piotr 10: Można szerzej ?

Piotr 10:

	6−n
xw(n)=
	−6

I teraz

	6−n		6−n
yw(n)=−3*(		)2+(n−6)*		+5
	−6		−6

?

Mila: a=−3<0⇔dla każdej z tych funkcji można obliczyc wartość największą− parabola skierowana w dół.

	−b		n−6
xw=		=
	2a		6

y_w=f_n(x_w)=...

Mila: Dobrze.

Piotr 10: Ok. Dziękuję, już dalej sobie poradzę

Piotr 10: Wyszło mi, że

	n2−12n+96
yw(n)=
	12

I jak mam ten wykres narysować ?

Piotr 10: Albo tak wiemy, że n∊N₊ Więc wykresem funkcji będzie będą ''punkty'' tak ? n=1,2,3,4,5,6,7,8,9,10,11,12 tak ?

Mila: Oblicz wartość y_w, mam inny wynik

	n−6
Xw=		tak będzie wygodniej liczyć.
	6

Piotr 10:

	n−6
Jutro wrócę do tego zadania, też wstawiłem za xw=		, jutro jeszcze raz to policzę
	6

Piotr 10:

	n−6)		(n−6)		n2−12n+36		n2−12n+36
yw(n)=−3(		)2+(n−6)*		+5= −3*		+		+5=
	6		6		36		6

	−n2+12n−36+2n2−24n+72+60		n2−12n+96
=		=
	12		12

Możesz Mila zerknąć ?

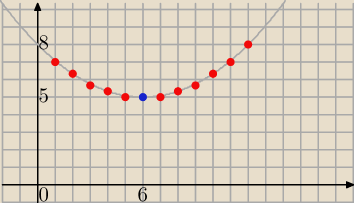
Mila: Dobrze, mogłeś od razu przedstawić w postaci kanonicznej, (wygodnie do narysowania ).

	−3		2
yw=		*(n−6)2+		*(n−6)2+5
	36		12

	1
yw=		(n−6)2+5
	12

Licz zbiór wartości:

	19
{7,		,....}
	3

Piotr 10: Wykresem funkcji będzie zbiór punktów tak ?

Mila: !2 punktów:

	19
{1,7),(2,		) itd
	3