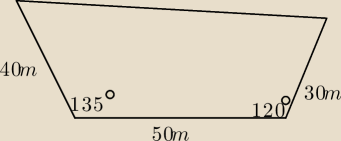Pole czworokąta Wiki: Oblicz pole powierzchni nieregularnego czworokąta, przedstawionego na rysunku

M:

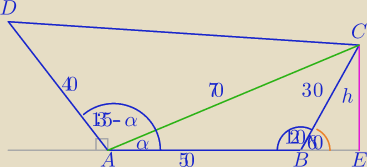Mila: 1) W ΔBEC: h=15√3 2)

	50*15√3
[ABC]=		=375√3
	2

3) z tw. cosinusów w ΔABC |AC|=70m

1
	*50*70*sinα=375√3 porównanie pola
2

	3√3		13
sinα=		, cosα=		, α− kąt ostry
	14		14

4) sin(135−α)=sin135^o*cos α− sinα *cos (135^o) sin(135−α)=.... oblicz

	1
[DAC]=		*40*70*sin(135o−α)
	2

5) P_ABCD=.[ABC]+[DAC]

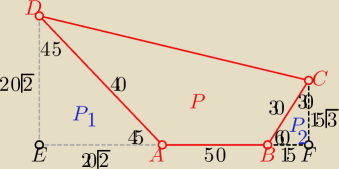Miki: P= P(trapezu EFCD) − (P₁+P₂)

	20√2+15√3
P(FECD)=		*(65+20√2)
	2

P₁=400

	225√3
P2=
	2

P=............

Mila: Pięknie, bez trygonometrii