geometria płaska Karooooo: wewnątrz kwadratu ABCD obrano p\y\taki punkt P, że trójkąt ABP jest równoboczny. Znajdź długość boku kwadratu , wiedząc że odległość punktu P od wierzchołka C jest równa √8+4√3. Wynik przedstaw w postaci m+n√3, gdzie m,n ∊C

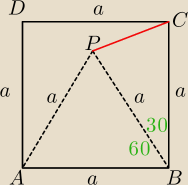
Mila: |PC|²=a²+a²−2*a*a*cos30

	√3
(√8+4√3)2=2a2−2a2*
	2

8+4√3=a²*(2−√3) /*(2+√3 (8+4√3)*(2+√3)=a²*(4−3) (28+16√3)=a² a²=4*(7+4√3) a²=2²*(2+√3)² a=2*(2+√3) a=4+2√3 Z jakiej to książki?

Bizon:

	a√3
h=
	2

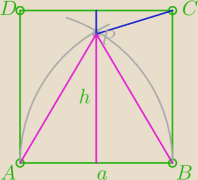
	a2		a√3
|PC|2=		+(a−		)2 ... i baw się −
	4		2