Indukcja jupijej: Witam. Mam problem odnośnie jednego zadania z indukcji matematycznej.

	n(n−3)
Pokaż przez indukcję, że n−kąt wypukły ma		przekątnych.
	2

Janek191:

	4*( 4 − 3)
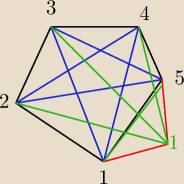
1o ) n = 4 czworokąt ma 2 przekątne oraz 2 =
	2

Wzór jest prawdziwy dla n = 4 2^o ) Zakładamy , że wzór jest prawdziwy dla n = k, czyli

	k*( k − 3)
liczba przekątnych jest równa
	2

Mamy pokazać, że z prawdziwości wzoru dla n = k wynika prawdziwość wzoru dla n = k + 1 Jeżeli liczba wierzchołków zwiększy się o 1 , to liczba przekątnych zwiększy się o ( k + 1) − 3 plus jeszcze 1 ( jeden bok będzie teraz przekątną ), czyli będzie ( k + 1) − 3 + 1 = k − 1 dodatkowych przekątnych. Razem będzie przekątnych

k*( k − 3)		k*(k −3)		2*( k − 1 )
	+ k − 1 =		+		=
2		2		2

	k2 − 3 k + 2k − 2		k2 − k − 2		( k +1)*[( k + 1) − 3]
=		=		=
	2		2		2

Na podstawie indukcji matematycznej wzór jest prawdziwy dla dowolnej liczby n ≥ 4.

Janek191: Na rysunku zamiast zielonej 1 powinna być zielona 6 (dodatkowy k + 1 wierzchołek ).

minka_xD: pszypadek? nie sondze ΔΔ

Janek191: Raczej przypadek − tak sądzę