Dziedzian i monotoniczność funkcji Funkcje:

x3		x4−12x2
	Obliczyłem, że dziedzina to (−∞;∞), a pochodna to
x2−4		(x2−4)2

Gdzie jest błąd? Bo wynik to (−∞;−2√3) u (∞;2√3)

Ajtek: Źle wyznaczona dziedzina. x²−4≠0 Pochodna na oko też nie wygląda za dobrze, ale mogę się mylić.

Funkcje: Fakt, granica to (−∞;2)(2;∞), ale reszty nadal niestety nie umiem:(

Ajtek: Nie granica, tylko dziedzina i nadal źle wyznaczona . Jak podstawię za x=−1 to w mianowniku otrzymam 1−4=3≠0 . Myśl.

Funkcje: proszę mi pomóc, bo już zrobiłem tyle tych przykładów, że chyba tutaj kolejnego wyniku nie dam rady zrobić..

Ajtek: Dasz radę

	f		f'*g−f*g'
(		)'=
	g		g2

Mariush: x²−4≠0 x²≠4 x≠2 x≠−2

Mariush: Ajtku,pomoz prosze mi)

Ajtek: Dziedzina okej. Teraz licz pochodną i więcej wiary w siebie

Mariush: chodzi mi o to: Przy jakim najmniejszym calkowitym znaczeniu parametru "a" rownanie ma tylko 2 rozne pierwiastki? √2x+13 * (√x2+18x+81 − √x2−10x+25) = a√2x+13

Funkcje:

	−x4+12x2
Wychodzi mi tak:
	(x2−4)2

Ajtek: Funkcje pokaż obliczenia .

Ajtek: Na początku pochodna policzona okej, w pierwszym poście. MOJE NIEDOPATRZENIE

Funkcje: Pomnożyłem przed ten (x²−4)², żeby zniknelo, a z reszty wyciagnalem x², nie wiem co dalej..

Ajtek: Masz wynik pochodnej:

	x4−12x2
f(x)'=...=
	(x2−4)2

Teraz f(x) rośnie gdy f(x)'>0, maleje gdy f(x)'<0. Zauważ, że mianownik zawsze jest >0. Badaj znak licznika .

Funkcje: Ale to nie muszę najpierw przyrównać tego do zera i rozwiązać ten układ?

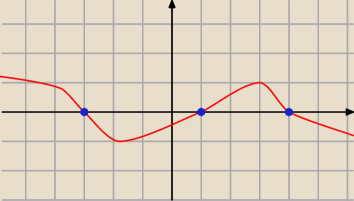
Ajtek: Szukasz monotoniczności. Możesz to przyrównać do zera, ale szkoda czasu. Masz to na rysunku przykładowym: f(x)'>0 rośnie, f(x)'<0 maleje, odczytujesz przedziały. Na czerwono wykres f(x)'. Przedziały co nad osią Ox, to f. rosnąca. Przedziały pod osią Ox, malejąca. To nie jest wykres Twojej pochodnej Jak przyrównasz do 0, to znajdziesz miejsca zerowe pochodnej (niebieskie kropki).

Funkcje: no tak, ale jak znaleźć te kropki bez przyrównania pochodnej do 0?

Ajtek: A jak znajdziesz kropkę taką: 2x>4

Funkcje: No właśnie nie wiem za bardzo, bo ja wszystko przyrównywałem i wtedy bez problemu wynik wychodził

Ajtek: Nosz kurka wodna 2x=4 2x>4 i 2x<4 widzisz coś

Funkcje: Poddaje się nie wiem, ale co jest źle w tym wyciąganiu przed nawias jeżeli chcę przyrównać do zera? bo ttamte metode chociaz potrafię w jakimś stopniu..

Ajtek: Rób, tak jak umiesz . W moim pytaniu chodziło mi o to: 2x=4 ⇔ x=2 2x>4 ⇔ x>2 i 2x<2 ⇔ x<2 Przyrównanie do zera pokazuje punkt "krytyczny" w tym przyadku x=2

Funkcje: O, teraz lepiej, a jaki miałem tam błąd?

−x4+12x2
	=0
(x2−4)2

Co tutaj pownienem po kolei zrobić? Mogę pomnożyć przez mianownik obie strony, a później zostałby licznik i wyciągnać 0 przed nawias?