ge RS: Wyznacz równanie takiej prostej przechodzącej przez punkt A (− 4,6) , która wraz z osiami układu współrzędnych ogranicza trójkąt o polu równym 2 A dalej nie wiem ? Co mam robić po kolej ?

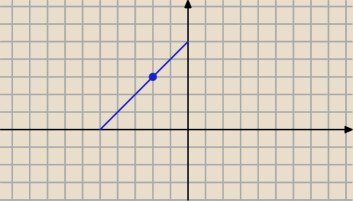
Godzio: y = ax + b, przechodzi przez punkt A więc b(a) = ... (przedstaw b za pomocą a) y = ax + b(a) A dalej, wyznacz punkty przecięcia z osiami:

	b(a)
A(−		,0) i B(0,b(a))
	a

	1		b(a)		b(a)2
P =				* b(a) =
	2		a		2a

RS: ?

Maslanek: Skoro ma ograniczać z osiami układu, to funkcja musi byc rosnąca. Czyli suzkamy prostej k: y=ax+b, gdzie a>0; b>0 Na pewno (−4,6) należy do k ⇒ 6=−4a+b ⇒ b=6+4a Wtedy k: y=ax+(6+4a)

	−6−4a
Należą do niej na pewno punkty: (0,6+4a) i (x0; 0) ⇒ x0=
	a

	−6−4a
Trójkąt, który powstaje jest prostokątny o przyprostokątnych (6+4a) i		.
	a

Reszta Twoja

RS: Godzio u Ciebie niestety nie przechodzi przez punkt A

Maslanek: Przechodzi, tylko Ty masz dopasować resztę

Godzio: Ja mam skalę 2,4,6 (a nie 1,2,3) dlatego wydaje Ci się, że nie przechodzi (a propo mojego, wprowadziłem kolizje oznaczeń, bo oznaczyłem A jako punkt przecięcia z osią, ale z tym sobie już poradzisz)

RS: Dziękuję Panowie, teraz już sobie poradzę

Bizon: ... a niby dlaczego ma być rosnąca ?

Maslanek: A nie musi byc faktycznie Może byc malejąca, ale dalej b>0

Godzio: Nie musi być, moje rozwiązanie nie wyklucza "malenia"

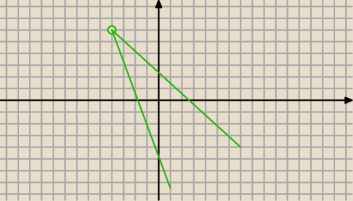
Bizon: ... tak poprowadzona prosta jak na rysunku Godzia w życiu nie utworzy z osiami trójkąta o polu równym 2

Bizon: ... b też wcale nie musi być większe od 0 −

Godzio: O matko, przecież to jest tylko szkic spokojnie

Bizon:

Bizon: ... Godzio ... to nie do Ciebie tylko do założeń Maślanka, że niby a>0 czy też b>0

Eta:

Maslanek: O tym nie pomyslałem Dawno się z geometrią nie widziałem

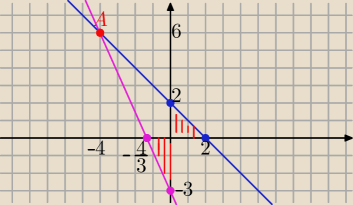
Eta: Można tak: Równanie odcinkowe szukanej prostej

	x		y
k:		+		=1 ⇒ bx+ay=ab i P= 2 ⇒ ab=4
	a		b

A(−4,6)∊k ⇒ −4b+6a=ab i rozwiązać układ równań .......

Bizon: ... i z zapominanego równania w postaci odcinkowej jest "najzgrabniej" −

Eta:

bezendu:

Eta: ?

bezendu: Pierwsze po lewej ?

Eta:

bezendu: i dobranoc

Eta: Już?

RS: Dziękuję.

Eta: Komu dziękujesz?

bezendu: Nie, dopiero o 02:00 ''jestem sową''

RS: Wszystkim w tym wątku.