Fiza
Theosh: Fizyka − kulki hardcore
Dwie kulki o masach m1 i m2 = 0,06kg stykały się razem wisząc na nici o długości 0,8m.
Kulkę m1 odchylono do poziomu jak to pokazano na rysunku i swobodnie puszczono. Zderzenie było
idealnie sprężyste a po odbiciu kulki wzniosły się na tę samą wysokość. Oblicz masę kulki m1.
Nie wiem jak to zrobić. Usiłuję zastosować zasady zachowania pędy i energii ale ta m1
uprzyksza mi zadanie na każdym kroku.
7 sty 21:26
Theosh:
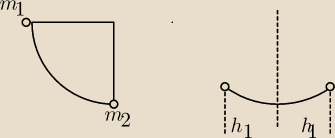
Zapomniałem rysunku ^^
7 sty 21:31
daras: a co ci przeszkadza m
1? po prostu podstaw do wzorów

7 sty 21:37
Theosh: Najpierw obliczam pe kulki w [ierwszym przypadku kiedy zostaje odchylona tzn.
p=m1√2hR
Teraz z zasady zachowania pędy wychodzi że m1√2hR = m1v1 +m2v2
Przy czym v1 i v2 oblicza się ze wzorów na odbicie sprężyste, ale i tak nie mam mas żeby to
zrobić( są wymagane) i nie wiem jak tam upchnąć te same wysokości jeszcze do tych wzorów.
7 sty 21:45
daras: prędkości różnią sie zwrotami wiec nie może być m1v1+m2v2
7 sty 21:46
daras: m2 masz podane
z ZZE: m1R=(m1+m2)h1
7 sty 21:48
Theosh: h1 nie jest dane
7 sty 21:51
daras: no to klops
7 sty 21:52
daras: wtedy jedyne rozwiazanie, które mi przychodzi do głowy:
m1 = m2
7 sty 21:52
Theosh: właśnie mi też bo energia potencjalna w tym przypadku od masy, bo przyspieszenie i wysokość ta
sama, ale jak to udowodnić...
7 sty 21:57
Maslanek: Dwa równania
1) z energii: m1gH=(m1+m2)gh
2) z pędu: m1 √2gH = (m2−m1) √2gh (prędkości po zderzeniu są równe, ale o przeciwnych
zwrotach − wynika z zasady zachowania energii)
Więc ostatecznie mamy:
m1H=(m1+m2)h
m1 √H = (m2−m1) √h
H mamy dane: H=0,8m (długość nici)
7 sty 23:10
daras: a czy ja napisałem coś innego o 21:48

8 sty 10:07
MQ: To zadanie napisał jakiś matoł, który nie ma pojęcia o fizyce. Jak widać z rysunków, pęd układu
przed zderzeniem nie będzie się równał pędowi po zderzeniu, więc nie będzie spełniona zasada
zachowania pędu.
Zadanie nie ma więc sensu.
8 sty 14:22
daras: sprawdź to na riki tiki tak

8 sty 15:32
Maslanek: W sumie tak. Zasadę zachowania pędu się zgodnie z kierunkami, nie?

daras, nie wiem, nie czytałem

8 sty 18:44
Maslanek: Nie no... Dlaczego nie będzie się równał?
Wystarczy, żeby m2>m1
8 sty 18:55
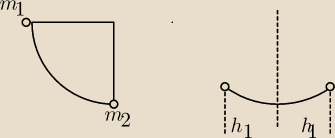 Zapomniałem rysunku ^^
Zapomniałem rysunku ^^



 daras, nie wiem, nie czytałem
daras, nie wiem, nie czytałem 