pomysł Dzionek95: Witam! Chciałbym zrobić układ 3 funkcji z czego jedna będzie kwadratowa i będzie ona przedstawiała uśmiech. Choć z definicji nie można tego nazwać funkcją... Zastanawiam się czy na przykład taki uśmiech mogła by przedstawiać y=3 i x należy (na przykład) <3;2> i tak samo y=2 i x należy tak samo <3;2> Macie może jakiś pomysł na równanie paraboli przekrzywionej o 90 stopni w lewo by była mniej więcej na takiej samej wysokości jak dwie proste, które tworzą oczy? Może jakiś pomysł by to usprawnić? Na pewno warto skorzystać z programu do rysowania funkcji tylko nie wiem jak się za to zabrać− więc jeśli coś to i tak będę kminił, bo odkąd dzisiaj wstałem to zacząłem myśleć o tej pierdole i teraz po powrocie ze szkoły zamiast się zająć prawdopodobieństwem to ta rzecz mi chodzi po głowie !

Ajtek: Pokombinuj z funkcją typu x=y²

Dzionek95: Jak ona mniej więcej wygląda, bo nie wiem czy efekt końcowy jaki mam na kartce będzie się pokrywał z jej faktycznym stanem. Nigdy w mojej 12letniej edukacji się nie spotkałem z takową

Dzionek95: Najbardziej chcę by to miało sens dlatego takie pytania/prośby

Ajtek: Obróć układ współrzędnych o 90^o (zeszyt) i narysuj zwykłą parabolę .

Dzionek95: Pi razy drzwi coś się kluje, mam problem z odczytaniem wartości b, ale ściągam program do rysowania funkcji i będę metodą prób i błędów to robił. Może jakaś wskazówka by to miało jeszcze lepszy efekt niż ma teraz ?

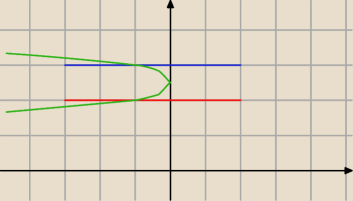
Ajtek: Ten twór będzie wyglądał mniej więcej tak .

Dzionek95: Podzielisz się tajemną wiedzą i napiszesz mi jaki wyszedł Ci wzór zielonej funkcji?Za Jej poszerzenie(rozjechanie) będzie odpowiedzialne a tak? A w ułamku jakimś małym 1/100?

Ajtek: To jest x=−y² (chyba) przesunięte o jakiś wektor. Tylko narysowałem to. Przy zielonej funkcji D: y∊R, natomiast zbiór wartości odczytujesz po osi Ox.

Ajtek:

	2+3
yw=
	2

	x1+x2
Bo masz dwie proste: y=2 i y=3. Dokładnie tak samo jak w zwykłej paraboli: xw=
	2

gdzie f(x₁)=f(x₂)

Dzionek95: Jest jakiś program, który po narysowaniu funkcji daje nam jej równanie? Morduję się z przesunięciemwierzchołka po narysowaniu takiej funkcjix=−1/25y² by ten wierzchołek był pomiędzy tymi dwoma funkcjami liniowymi czyli by był on na osi Ox 2,5 z tego co widze z wykresu− jakieś sugestie ?

Ajtek: Nie mam zielonego pojęcia, czy jest jakiś program. Może wolfram pomoże.

Dzionek95: No to jak psioczyłem na inne programy online tak ten mnie zabił, chyba jednak wrócę do zadań na sprawdzian i sobie daruje chyba, że ktoś jeszcze rzuci jakieś nowe światło na tą całą beznadziejną sprawdę Diekuję Ajtek i tak za pomoc

Ajtek: To inaczej: masz 2 proste x=2 i x=3, x_w znane i dajmy na to f(x₁)=f(x₂)=1 Znajdź wzór tej funkcji y=...., później zamień x z y. Może to coś da .

Dzionek95: y=−1/25x²−1/5x−3 do takiego czegoś doszedłem biorąc wyraz wolny na oko by akurat w tym miejscu przeciął się z osią a resztę metodą prób i błędów wzorkiem na wierzchołek. Coś już tutaj mam, możesz to ewentualnie sprawdzić co spłodziłem ?

Dzionek95: y=−1/25x²−1/4x−3 wygląda lepiej i teraz zmienić dwie funkcje linowe na 4 i 3? Co myślisz mój drogi internetowy matematyku ?

Ajtek: Słuchaj, ja tutaj też improwizuję .

Dzionek95: Jak mi to pyknie dasz mi swoje dane i podeśli Ci dobrą ćwiartkę żebyś też się mógł uśmiechnąć ! Możesz tylko zyskać !

Ajtek: Beż ćwiartki też się obejdzie .

Dzionek95: Oki Reasumując wrzucając do układu 3 równania funkcji mamy: y=4 , x∊<4;6> y=2 , x∊<4;6> x=−1/25y²−1/5y−3 y∊<0;5> Daje tak samo jak mi na kartce uśmieszek a dokładnie taki "=)"

Ajtek:

Dzionek95: Dzięki, dzięki, dzięki− pomogłeś mi zasnąć i mam nadzieję uśmiech nauczycielki ! Wiadomo, że uśmiech jest bezcenny, więc dzięki + 2kπ