Algebra zbiorów Wojciecj: Sprawdzić ,że dla dowolnych zbiorów A, B, C , jeżeli A = A ∩ B , to A ⊂ B 2 Przykład Sprawdzić, że dla dowolnych zbiorów A, B, C prawdziwa jest równość A ∪ ( A ∩ B ) = A

Wojciech:

Eta: L=x∊AU(A∩B)⇔x∊A v x∊(A∩B)⇔x∊A v (x∊A⋀x∊B)⇔(x∊A v x∊A )⋀(x∊Av x∊B)⇔x∊A=P

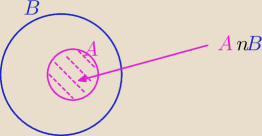
Eta: A⊂B ⇒ ( A∩B=A)

Eta: Można też tak: 1/ x∊(A∩B) ⇔x∊A⋀x∊B⇔x∊A ⇒ A⊂B

wredulus_pospolitus: Albo tak: A=A∩B ⇔ ∄_x∊A x∊A∩B ⇒ ∄_x∊A x∊B ⇒ A⊂B

Eta: