nierówność Robert: Witam, mam mały problem z taką nierównością. Gdzieś mieszam minusy, bo przy rysowaniu wykresu widzę błąd.

1		1
	≥
x2 − 5x + 6		2

Janek191:

1		1
	≥		/ * 2
x2 − 5x + 6		2

2
	≥ 1
x2 − 5x + 6

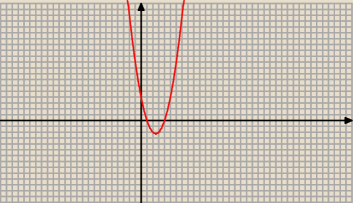
2 ≥ x² − 5 x + 6 ⇒ 0 ≥ x² − 5x + 4 ⇒ x² − 5x + 4 ≤ 0 Δ =25 − 4*1*4 = 9 ⇒ √Δ = 3

	5 − 3		5 + 3
x1 =		= 1 x2 =		= 4
	2		2

a = 1 > 0 → ramiona wykresu funkcji f(x) = x² − 5x + 4 są skierowane ku górze ⇒ x ∊ ( 1; 4 ) =========

Bizon: np tak:

1		1
	≥
(x−2)(x−3)		2

Dziedzina a potem można się bawić w dwóch przedziałach

Janek191: Dodatkowo x ≠ 2 i x ≠ 3 więc x ∊ ( 1 ; 4) \ { 2, 3 } ================

Janek191: Źle rozwiązałem

pigor:

	1		1
hmm..., no to np. tak :		≥		⇔
	x2−5x+6		2

	1		1
⇔		−		≥0 /2(x−3)2(x−2)2 ix∊R\{3,2}=Dn(*) ⇔
	(x−3)(x−2)		2

⇔ 2(x−3)(x−2)− (x−3)²(x−2)² ≥0 ⇔ (x−3)(x−2)(2−x²+5x−6) ≥0 ⇔ ⇔ (x−3)(x−2)(−x²+5x−4) ≥0 /*(−1) ⇔ (x−3)(x−2)(x²−5x+4) ≤ 0 ⇔ ⇔ (x−3)(x−2)(x−1)(x−4) ≤ 0 , więc stąd i z (*) ⇔ x∊[1;2) U (3;4] . ...

Robert: Wielkie dzięki, po prostu gubiłem minus i odwrotnie parabolę narysowałem. Mam jeszcze dwa przykłady, będę bardzo wdzięczny nawet za wskazówki:

|2x|		|x+1|
	≥ 3 i		< 1
|x2 − 3|		|x−2|−2

Robert: Jakieś małe naprowadzenie ?

pigor: ..., np. tak : 1) U{|2x|}{|x|²−3| ≥ 3 /*|x²−3| i x²≠3 ⇔ 2|x| ≥ 3|x²−3| i |x|≠ √3 ⇔ ⇔ |3(x²−3)| ≤ 2|x| /² i (*) x≠±√3 ⇒ (3x²−9)²−(2x)² ≤ 0 ⇔ ⇔ (3x²−9−2x) (3x²−9+2x) ≤ 0 ⇔ (**) (3x²−2x−9) (3x²+2x−9) ≤ 0 i masz wredną nierówność, bo 2 brzydkie trójmiany w nawiasach o wspólnym wyróżniku Δ=4+4*27= 4*28= 16*7 i p{Δ)= 4√7, wtedy ich pierwiastki n[x_1,2= ¹₆(2±4√7)]] v x_3,4= ¹₆(−2±4√7) , no to teraz narysuj sobie oś Ox, oszacuj na kalkulatorze położenie na niej tych x_1,2,3,4 i "pobaw się" z wykresem tej nierówności (**) pamiętając o (*) . ... −−−−−−−−−−−−−−−−−−−−−−−−−−−−− p.s. sprawdź czy nie walnąłem się gdzieś , za co z góry przepraszam, bo znikam do wieczora

pigor: o kurcze ,już na samym początku nie dopiąłem klamrą } ułamka

Eta: Za to .... reszta jest ok