szkicowanie wykresu minka_xD: mam do naszkicowania wykres o ponizszych danych: 1. a) f'(x) > 0 dla x ∊ (−∞; 1) b) f'(x) < 0 dla x ∊ (1; ∞) i tutaj mam problem: c) lim f(x) = f(1) x −> 1 jak sobie poradzic z pkt 3? jak to zinterpretowac? 2. a) f'(x) > 0 dla x ∊ (−∞; 1) b) f'(x) < 0 dla x ∊ (1; ∞) f nie ma ekstremum w x = 1 to ze nie ma ekstremum znaczy, ze 1 nie nalezy do dziedziny tak?

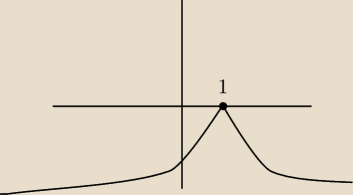
minka_xD: czy 1. moze byc takie? to lim f(x) = f(1) to jak rozumiem znaczy ze funkcja jest ciagla

wredulus_pospolitus: (1) może być ... aczkolwiek lepiej (bezpieczniej) by było narysować parabole (ramiona skierowane do dołu) ze względu na to, że funkcja którą narysowałeś/−aś NIE MA pochodnej w punkcie x=1 (co prawda w treści zadania nie ma o tym słowa −−− ale trzeba o tym pamiętać) (2) niekoniecznie (może należeć do dziedziny) −−−− ale ... ale w puncie x=1 występuje 'nieciągłość' funkcji