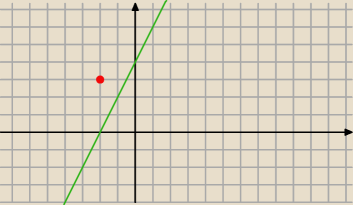
A takie tam. bezendu: Mam podany punkt P=(−2,3) i prostą k:y=2x+4 jak znaleźć prostą k' która jest obrazem symetrii prostej k względem punktu P ? Proszę o wytłumaczenie.

Saizou : znajdź prostą równoległą do prostej zielonej równo oddalonej od czerwonego punktu

bezendu: Odległość punktu P od prostej k

	|4+3−4|
d=
	√5

	3√5
d=
	5

prosta równoległa y=2x+b ?

bezendu: No i co dalej ?

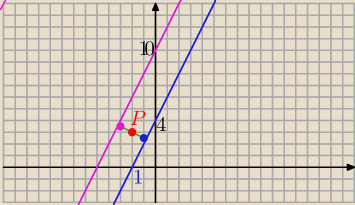
Marcin: To jest prosta przesunięta o wektor = [2;2] czyli będzie miała równianie y=2(x+2)+6 →y=2x +10

bezendu: Czemu o taki wektor?

Eta: P(a,b)

x+x'
	=a ⇒x+x'= 2a ⇒ x'= 2a−x
2

y+y'
	=b ⇒y+y'= 2b ⇒ y'=2b−y
2

k^' : 6−y^'=2(−4−x^') +4 ( uporządkuj i opuść "primy" k^' : y= 2x+10

bezendu: Dziękuję. Jutro będę analizował.

bezendu: Nie rozumiem przed ostatniej linijki.

bezendu: Może ktoś to wytłumaczyć k': 6−y=2(−4−x)+4 ?

bezendu: ?

bezendu:

MQ: Bo: y=2x+4 y=2b−y' b=3 więc y=6−y' x'=2a−x a=−2 więc x=−4−x' Podstawiasz do pierwszego i masz: 6−y'=2(−4−x') +4

bezendu: Dzięki !

Mila: W symetrii środkowej względem punktu S(a,b)=(−2,3) obrazem punktu P(x,y) jest punkt P'(x',y'), gdzie: x'=2a−x y'=2b−y ⇔a=−2, b=3 x'=2*(−2)−x ⇔(1) x'=−4−x y'=2*3−y ⇔(2) y'=6−y Prosta y=2x+4 została przez tę symetrię przekształcona obliczamy xi y z wzorów (1) i(2) x=−x'−4 y=−y'+6 podstawiamy do rownania prostej −y'+6=2*(−x'−4)+4 −y'=−2x'−8+4−6⇔−y'=−2x'−10 y'=2x'+10 ⇔y=2x+10 To bardzo ogólna metoda, tu wystarczyło znaleźć obraz jednego punktu z prostej k, spróbuj tak zrobić

bezendu: Wyznacz równanie okręgu symetrycznego do okręgu x²−6x+y²+4y=27 względem prostej y=1 (x−3)²−9+(y+2)²−4=27 (x−3)²+(y+2)²=40 A tutaj jak to zrobić ?

matyk: Odbij tylko środek. Promień zostaje ten sam.

bezendu: (x+3)²+(y−2)²=40

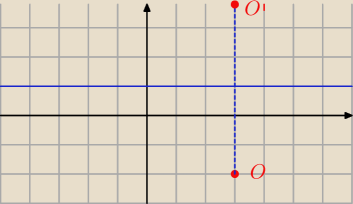
MQ: Nie, (x−3)²+(y−4)²=40

bezendu: MQ czemu y−4 ?

MQ:

bezendu: A no racja mój błąd. Dziękuję.