. Piotr 10: Ze skończonego ciągu kolejnych liczb naturalnych nieparzystych 1,3,5,.....,2n−1 wybieramy kilka kolejnych liczb końcowych, których suma wynosi 120. Różnica kwadratów największej i najmniejszej z wybranych liczb jest równa 360. Znajdź wybrane liczby. Od czego zacząć ? a²−b²=360 (a−b)(a+b)=360 I tutaj jakoś kombinować wpierw?

matyk: Wykorzystaj drugą informację także

Piotr 10: No właśnie coś ciężko, ''kilka kolejnych liczb końcowych'' i za bardzo tego ruszyć nie mogę

PW: k kolejnych liczb końcowych to (patrząc od tyłu) 2n−1, 2n−2, 2n−3, ... (i kończymy na ...)

Piotr 10: No dobra 2n−1+2n−2+2n−3+.....=120 (2n−1)² − (?)=360

Piotr 10: Albo chyba wiem Zliczyć sumę 2n−1, 2n−2, 2n−3 .. to ciąg o różnicy −1 S_k=.. tak ?

Piotr 10: Pomoże ktoś ?

Piotr 10: ?

Piotr 10: ?

Mila: Liczby: 1,3,5,7,9,...2n−1 tworza c. arytmetyczny o różnicy r=2, ciąg rosnący

	1+2n−1
Sn=		*n suma wszystkich wyrazów, masz n wyrazów
	2

S_n=n² S_k− suma k początkowych wyrazów , k<n

	1+2k−1
Sk=		=k2
	2

S_n−S_k=120⇔n²−k²=120 Suma wyrazów: a_k+1,a_k+2,...a_n jest równa 120 Najmniejszy wyraz ma numer {k+1} a_k+1=2*(k+1)−1=2k+1 Drugi warunek: (2n−1)²−(2k+1)²=360 stąd ( rozwiąż, korzystaj z wzorów skróconego mnożenia ) k=13 n=17 Masz 17 wszystkich wyrazów, Zsumowano wyrazy: a₁₄,a₁₅,a₁₆,a₁₇ czyli: 2*14−1=27, 29,31,33 Spr. 27+29+31+33=120 33²−27²=(33−27)*(33+27)=6*60=360

Piotr 10: Dziękuję bardzo

Mila: Skąd to zadanie?

Piotr 10: Od pani ze szkoły, z powtórzenia do matury

Mila: Można to zadanie rozwiązywać "na piechotę". 1) Sumujesz dwie ostatnie liczby i sprawdzasz warunek z różnicą kwadratów. 2) Sumujesz 3 ostatnie liczby i sprawdzasz warunek z różnicą kwadratów. itd zobacz tym sposobem

Piotr 10: Na razie analizuje Twoje rozwiązanie pierwsze . Jeszcze mam jedno zadanie, którego za bardzo też nie wiem jak zrobić

Mila: Napisz, teraz nie rozwiążę, bo zaraz mam gosci. Później.

Piotr 10: Końcami odcinka są punkty A(−1;−2) i B(3;6). Odcinek CD jest obrazem odcinka AB zarówno w jednokładności o środku S₁(−5;2) jak i w jednokładności o środku w punkcie S₂=(3;2). Oblicz współrzędne końców odcinka CD i skalę jednokładności o środku w punkcie S₂. Te wydaję się łatwiejsze od poprzedniego, ogólnie rozumiem jednokładność. Ale tutaj jakoś nie mogę, próbowałem układ równań ale nie za ciekawie później było. Ok poczekam

matyk: Dobry rysunek zrób

Piotr 10: Spoko matyk już prawie te zadanie z ciągiem zrozumiałem, a potem jeszcze trapezik z wczoraj co mi pomagałeś i dopiero to zadanko

Piotr 10: Mila a tutaj '' Suma wyrazów: a_k+1,a_k+2,...a_n jest równa 120'' nie powinno być na końcu a_2n−1 ?

Mila: 2n−1 to jest wartość n−tego wyrazu a nie indeks.

Piotr 10: OK. Dziękuję

Piotr 10: Mila to pomożesz z tym zdaniem z postu 7 sty 18:34 ? Takie coś napisałem S₁C^→=k₁*S₁A^→ S₁D^→=k₁*S₁B^→ S₂C^→=k₂*S₂A^→ S₂D^→=k₂*S₂B^→

Mila: Za godzinę.

Piotr 10: Ok, to idę robić inne zadanka

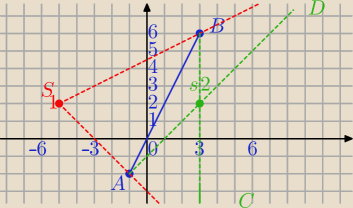
Mila: S₁ jest środkiem jednokładności o skali dodatniej C=J^k1(A) D=J^k1(B) i k1>0 stąd S₁C^→=k1*SA^→ i S₁D^→=k1*SB^→ pierwsze dobrze Drugie tak: Dla s₂ i k2<0 mamy tak C=J^k1(B) D=J^k1(A) S₁C^→=k2*SB^→ i S₁D^→=k2*SA^→ II sposób Współrzędne punktu C możesz łatwo znaleźć jako punkt przecięcia prostych x=3 i prostej SA, wtedy będziesz miał skalę i dodatnią i ujemną Prosta SA: y=−x−3 C=(3,−6) dokończ

Mila: Ma być C=J^k2(B) D=J^k2(A) Kopiowałam i nie zmieniłam indeksów.

Piotr 10: Ok. Dziękuję