l Radek: W urnie znajduje się 27 kul w dwóch kolorach. Wiadomo, że wśród każdych 13 kul wybranych z urny jest co najmniej jedna czarna, a wśród każdych 16 kul jest co najmniej jedna biała. Ile białych kul znajduje się w urnie?

Radek: ?

matyk: Proponuje wziąć 27 piłek do tenisa i malować je

matyk: A tak serio to 12

Radek: Ze zbioru {1,2,3,...,1996 } losujemy jedną liczbę. Oblicz prawdopodobieństwo, że wylosowana liczba jest podzielna przez 4 lub 6 lub 10 policzyłem ile jest podzielnych przez 4 ile jest podzielnych przez 6, ile podzielnych przez 10 przez 10−199 przez 4−499 przez 6−332 i teraz mam policzyć ile jest podzielnych przez 4,6,i 10 ?

Radek: A jak do tego doszedłeś ?

Radek: ?

matyk: wśród każdych 13 jest jedna czarna = czarnych jest przynajmniej 15 wśród każdych 16 jest jedna białą = białych jest co najmniej 12 Ale wszystkich jest 27 czyli 12+15 ⇒ białych jest dokładnie 12

matyk: Zadanie drugie. Wykorzystujemy tzw. zasadę włączeń i wyłączeń: Korzystamy z wzoru: |A ∪ B ∪ C|=|A|+|B|+|C|−|A ∩ B|−|B ∩ C|−|A ∩ C| + |A ∩ B ∩ C| Jeszcze brakuje ci doliczyć |A ∩ B| |B ∩ C| |A ∩ C| |A ∩ B ∩ C|

Radek: @matyk ale patrz policzyłem ile jest podzielnych przez 6 przez 10 przez 4 przez 4,6,10 i teraz jeszcze brakuję 4,10 i 6,10 ?

matyk: i jeszcze przez 4 i 6 Potem podstaw do wzoru, który ci dałem

Radek: Ok

reon:

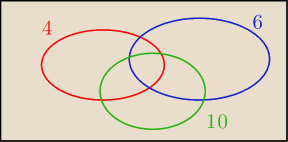
Trivial: A tutaj graficzna reprezentacja tego wzoru (tzw. diagram Venna).

Radek: Coś nie wychodzi poprawne rozwiązanie podzielnych przez 6−332 podzielnych przez 4−499 podzielnych przez 10−199 podzielnych przez 4,6−166 podzielnych przez 4,10−49 podzielnych przez 6,10−66 podzielnych przez 4,6 i 10−33 332+499+199−166−49−66−33=716

	716		179
P(A)=		=
	1996		499

Ale jest źle

Radek: ?

Trivial: Na końcu ma być +33.

Radek: to jak dodam to już kompletnie zły wynik wychodzi.

Radek: ?

matyk: przez 4 i 10 masz źle policzone

Trivial: Tych liczb jest 732. http://ideone.com/MXDh39 Podzielnych przez 4: [1996/4] = 499 Podzielnych przez 6: [1996/6] = 332 Podzielnych przez 10: [1996/10] = 199 Podzielnych przez 4,6: [1996/(4*3)] = 166 Podzielnych przez 6,10: [1996/(6*5)] = 66 Podzielnych przez 4,10: [1996/(4*5)] = 99 Podzielnych przez 4,6,10: [1996/(4*3*5)] = 33 |A| = 499 + 332 + 199 − 166 − 66 − 99 + 33 = 732.

matyk: gdzie znak [] − oznacza część całkowitą (podłoga)

Radek: Ale czemu A∩B∩C się dodaje a nie odejmuje ?

Trivial: Zobacz na obrazku. Na początku dodajemy wszystkie zbiory (4∪6∪10), ale niektóre części dodaliśmy parę razy. Takimi częściami są zbiory 4∩6, 4∩10, 6∩10. Odejmujemy je. Część 4∩6∩10 dodaliśmy 3 razy, a potem 3 razy odjęliśmy − jest zatem uwzględniona 0 razy. Korygujemy to poprzez dodanie jej do końcowego wyniku.

Trivial: matyk, no pewnie.

Radek: Dzięki a czym różnic się zapis A⊂B A⊆B ?

Trivial: W zależności od upodobań osoby może się różnić, ale nie musi. Niektórzy używają zapisu A⊂B tylko na oznaczenie podzbioru właściwego (czyli jako: A⊂B ⇔ A⊆B ∧ A≠B).

Radek: Dzięki po raz n

Trivial: A tutaj więcej: http://pl.wikipedia.org/wiki/Podzbi%C3%B3r#Zapis