f(x)=[x]+x agnieszka: wykres funkcji f(x)=[x]+x gdzie [x] to część całkowita liczby x jak narysować taki wykres ?

matyk: W przedziałach najlepiej Weźmy przedział [0,1) Dla niego podłoga wynosi 0. Zatem mamy funkcję y=x

agnieszka: a co dla np x=1¹₂ ?

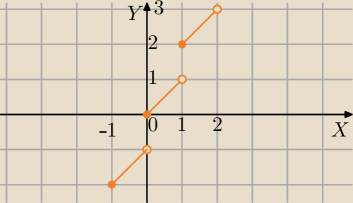
Mila: 1) Dla x∊<0,1) f(0)=[0]+0=0 f(0,5)=[0,5]+0,5=0+0,5=0,5 f(x)=[x]+x=0+x f(x)=x

	3		3		3		3		1
2) dla x∊<1,2) f(		)=[		]+		=1+		=2
	2		2		2		2		2

[x]+x=1+x 3) dla x∊<−1,0 ) f(−1)=[−1]+(−1)=−2 f(x)=−1+x

	−1		−1		−1		1		−3
f(		)=[		]+(		)=−1−		=
	2		2		2		2		2

itd

pL: a co jesli bede mial {x}+x {x}i czesc ulamkowa ?

Kaja: Udowodnij, że jeżeli a jest dowolną liczbą dodatnią to funkcja f \left( x \right) = x³ + ax +1 jest rosnąca w zbiorze liczb rzeczywistych