prawd Radek: W garderobie pani Joanny wiszą 3 żakiety: biały, zielony i granatowy oraz 4 spódnice: czarna, biała, granatowa i szara. Oblicz prawdopodobieństwo zdarzenia, że wybierając losowo jeden żakiet i jedną spódnicę, pani Joanna skompletuje strój w jednym kolorze

	1		1		1		1		1
P(A)=		*		+		*		=
	3		4		3		4		6

Jak inaczej to zapisać ?

martin: |Ω|=12 |A|=2 P(A)=2/12=1/6

Radek: A i B są takimi zdarzeniami losowymi zawartymi w Ω , że A ⊆ B oraz P (A ) = 0,3 i P(B ) = 0,7 . Oblicz prawdopodobieństwo różnicy B ∖ A . nie za mało danych ? Proszę o wytłumaczenie

martin: mozliwosci wyboru zakietu sa 3, a spodnicy 4 a wiec wszystkich mozliwosci jest 3*4=12 mozliwosci wyboru pod kolor sa tylko dwie− biały i granatowy

martin: https://matematykaszkolna.pl/strona/3243.html

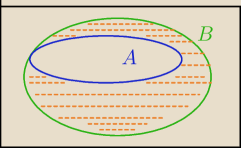
Mila: P(A)=0,3 P(B)=0,7 P(B\A)=P(B)−P(A∩B)=P(B)−P(A)=0,7−0,3=0,4

Radek: Dziękuję nie za bardzo rozumiem te diagramy venna jeszcze.

Radek: W dwóch pudełkach są cukierki. W pierwszym pudełku jest 15 cukierków czekoladowych i 5 owocowych, a w drugim pudełku jest 20 cukierków czekoladowych i 30 cukierków owocowych. Losujemy cukierek najpierw z pierwszego, a potem z drugiego pudełka. Jakie jest prawdopodobieństwo, że w wyniku losowania otrzymamy dwa cukierki czekoladowe? Można zrobić na dwa drzewka ?

	3
Wyszło
	10

	20 1		19!*20
Albo Ω=		=		=20
			19!*1!

	15 1
A=		=15

	15		3
P(A)=		=
	20		4

	50 1
Ω=		=50

	20 1
B=		=20

	20		2
P(B)=		=
	50		5

I to mnożymy a kiedy byśmy dodawali ?

Mila:

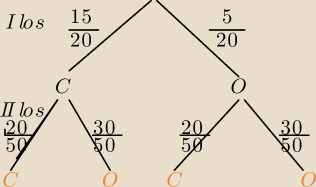
	15		20		3		2		3
P(CC)=		*		=		*		=
	20		50		4		5		10

Wylosowano cukierek czekoladowy i owocowy, wtedy suma Napisz jaka?

matyk: Kiedy pytalibyśmy np. o wynik losowania w którym otrzymamy co najwyżej jeden cukierek czekoladowy. Chociaż tutaj można ze zdarzenia przeciwnego i pomijamy dodawanie sytuacji. Dodajemy wyniki do siebie gdy mówimy o kilku rozłącznych różnych przypadkach. To tak w skrócie

matyk: Jak słusznie podała Mila gdy idziemy z "góry na dół" mnożymy, gdy idziemy na boki dodajemy

Radek: 1

Radek: W jednej urnie są 3 kule: czerwona, biała i zielona, a w drugiej urnie są 2 kule: czerwona i biała. Losujemy po jednej kuli z każdej urny. Jakie jest prawdopodobieństwo wyciągnięcia dwóch kul w tym samym kolorze? Mogę od razu tak:

	1		1		1		1		1
P(A)=		*		+		*		=		?
	3		2		3		2		3

Mila: B− wylosowano cukierek czekoladowy i owocowy

	15		3		5		2		11
P(B)=		*		+		*		=
	20		5		20		5		20

19:24 Dobrze.

Radek:

	1
Rzucamy trzema kostkami. Prawdopodobieństwo otrzymania sumy oczek równej 3 wynosi		, a
	216

	1
prawdopodobieństwo otrzymania sumy oczek równej 4 wynosi		. jakie jest
	72

prawdopodobieństwo tego, że suma otrzymanych oczek będzie mniejsza od 5?

daras: moze najpierw ustalmy: co to jest żakiet?

Radek: ?

Mila: Radek to zadanie z 19:45. To dokładnie taka treść, czy Twoja twórczość? Pomyśl, kiedy otrzymasz sumę oczek<5?.

Radek: To jest dokładna treść zadania. (1,1,1) (1,1,2) Jak takie możliwości wypadną

Mila: W takim razie masz dwa zdarzenia rozłączne: A− suma oczek równa 3 B− suma oczek równa 4

	1		1
P(AUB)=P(A)+P(B)=		+
	216		72

Gdyby nie było informacji o tych prawd., to tak: |Ω|=6*6*6=216 C− suma oczek mniejsza od 5 C={(1,1,1), (1,1,2),(1,2,1),(2,1,1)}

	4		1
P(C)=		=
	216		54

Radek: Ale tam jest ta informacja i nie wiem jak z niej skorzystać ?

Radek: ?

Mila: To masz wyjaśnione przed słowem "gdyby". Suma oczek mniejsza od 5⇔suma oczek 3 lub 4