Ciągi O.O:

	n−1
Ciąg an określony jest wzorem an=		. Wynika z tego, że różnica ak+1−ak−1 jest
	n

równa:

	2
A.
	k2−1

	k+1
B.
	k2−1

	2(k2+2k−1)
C.
	k+1

	k2−1
D.
	2

Proszę o odpowiedź

ZKZ: Moze nie odpowiedz a podpowiedz

	k−1
ak=		i teraz licz roznice
	k

O.O: Z tego wychodzi mi wynik 2, nie mam pojęcia dlaczego

ZKZ: A jak to liczysz −pokaz

O.O:

k−1		k−1
	+ 1 − (		−1)
k		k

O.O: i sprowadzam do wspólnego mianownika i nic mi nie wychodzi

ZKZ: Tak to sie nie liczy

	k−1
Chcac obliczyc wyraz ak+1 do wzoru ak=		w m mmiejsce k wstawiasz k+1 wtedy
	k

	k+1−1		k
otrzymamy ak+1=		=
	k+1		k+1

POlicz teraz tak samo wyraz a_k−1= wmiejsce k dowzoru na wyraz a_k wstwa k−1

bezendu: 5−latek ?

ZKZ: ja poczekam

O.O: dzięki za pomoc

O.O: ale mam jeszcze jedno, choć to inna dziedzina, pomożecie z trygonometrii?

O.O:

	sinα+sinβ
Wykaż, że gdy α i β są kątami ostrymi trójkąta prostokątnego, to		=1
	cosα+cosβ

O.O: Próbowałem i nic z tego, np. pomnożyć obustronnie przez cosα+cosβ przy założeniu że nie równa się 0, ale korzystając z metody nie wprost wychodzi coś typu sinα+sinβ ≠ cosα+cosβ, proszę o pomoc

ZKZ: Juz mnie o to pytal RS Brat Krzysiek bedzie jutro na forum jak wroci od corki

ZKZ: Przeciez nie skonczyles tamtego zadania

O.O: Albo coś tu jest nie tak, albo nie mam pojęcia jak to zrobić.

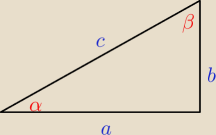
Ajtek: sinα=... sinβ=... cosα=... cosβ=...

O.O: Tamto zadanie już potrafię wykonać

O.O:

	b
sinα =
	c

	a
sinβ =
	c

	a
cosα =
	c

cosβ = {b}{c}

O.O:

	b
cosβ =		**
	c

ZKZ: Dobrze

Ajtek: I jedziesz

O.O: I teraz powstawiać te literki pod ten wzór? To tyle?

O.O: Myślałem, że metoda nie wprost mnie nie zawiedzie [*]

O.O: Dla ciekawskich odpowiedź do ciągów to A

ZKZ: Rowniez podziekuj Ajtkowi

O.O: Dzięki wielkie, zaraz zobaczę co z tego wyjdzie!

Ajtek: Mam nadzieję, że 1