Maturalne
bezendu:
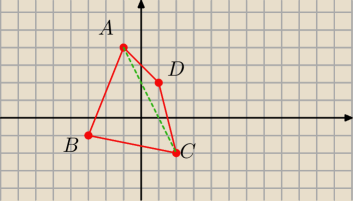
Dany jest czworokąt ABCD , gdzie A=(−1,4), B=(−3,−1), C=(2,−2), D =(1,2)
oblicz :
| | sin∡DBC | | sin∡DBA | |
( |
| )2+( |
| )2 |
| | sin∡BCD | | sin∡BAD | |
policzyłem to z twierdzenia cosinusów i wyznaczyłem sin ale bardzo dużo obliczeń. Jest jakiś
krótszy sposób ? Zadanie nie jest trudne.
4 sty 19:54
bezendu:
Ma ktoś jakiś inny pomysł oprócz mojego ?
4 sty 20:07
Bizon:
... a dlaczego z twierdzenia cosinusów ... może lepiej z sinusów −
4 sty 20:36
Saizou : albo wzór na tgx między prostymi
4 sty 20:42
bezendu:
Dzięki Panowie
4 sty 20:44
Bizon:
| | sin∡DBC | | sin∡DBA | |
( |
| )2+( |
| )2= |
| | sin∡BCD | | sin∡BAD | |
4 sty 20:48
Mila:
Jaki ma być wynik?
4 sty 20:53
bezendu:
Mila 1
4 sty 20:58
Mila:
Tam masz podpowiedź Bizona, to już nie piszę swojego rozwiązania .
4 sty 21:06
bezendu:
Mila takie zadanie Twoim zdanie może być na roz czy raczej za proste ?
4 sty 21:07
Saizou :
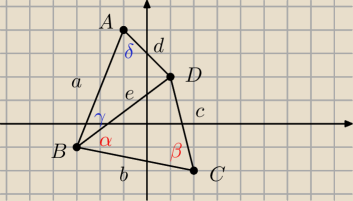
a ja dokończę, bo mi się nudzi
będzie dla potomnych
| | 1 | | 1 | | sinα | | c | |
PBCD= |
| eb*sinα= |
| bc*sinβ⇒e*sinα=c*sinβ⇒ |
| = |
| |
| | 2 | | 2 | | sinβ | | e | |
| | 1 | | 1 | | sinγ | | d | |
PABD= |
| ae*sinγ= |
| ad*sinδ⇒e*sinγ=d*sinδ⇒ |
| = |
| |
| | 2 | | 2 | | sinδ | | e | |
c
2=4
2+1
2=17
d
2=2
2+2
2=8
e
2=3
2+4
2=25
| | c | | d | | c2+d2 | | 17+8 | |
( |
| )2+( |
| )2= |
| = |
| =1 |
| | e | | e | | e2 | | 25 | |
4 sty 21:49
bezendu:
Wyszło Ci tak jak mi
4 sty 21:51
Mila:
Może być na R. To zadanie raczej zaliczyłabym do trudniejszych.
Sam widzisz, że liczyłeś sposobem czasochłonnym, są inne sposoby też wymagające sporo czasu, a
na maturze czas ograniczony.
4 sty 21:51
bezendu:
I dlatego właśnie pytałem o ten krótszy sposób.
4 sty 21:51
Mila:
Inaczej liczyłam. Jutro napiszę. Teraz Dobranoc.
4 sty 21:54
bezendu:
Szkoda, że tak szybko musisz uciekać z forum. Dobranoc.
4 sty 21:55
Mila:
Patrz na rysunek
Saizou.
e=5
d=2
√2
c=
√17
a=
W ΔDBC z tw. sinusów
| c | | e | | c | | sinα | |
| = |
| ⇔ |
| = |
| |
| sinα | | sinβ | | e | | sinβ | |
W ΔABD z tw. sinusów:
| | sinα | | sinγ | | c | | d | |
( |
| )2+( |
| )2=( |
| )2+( |
| )2= |
| | sinβ | | sinδ | | e | | e | |
| | √17 | | 2√2 | | 17 | | 8 | |
=( |
| )2+( |
| )2= |
| + |
| =1 |
| | 5 | | 5 | | 25 | | 25 | |
5 sty 16:49
bezendu:
Dziękuję, oczywiście przeanalizuję ten sposób.
5 sty 19:10
5-latek: Witam wszystkich
A ja jednak uwazam ze geometria analityczna opiera sie na wektorach
No ale dosc marudzenia .
Mamy wektor u=[a
1 b
1] i wektor v=[a
2 b
2]
Jest taki wzor na sinus kąta miedzy wektorami u i v
| | a1b2−a2b1 | |
sinφ= |
| gdzie |u| i |v| sa to dlugosci wektorow . |
| | |u|*|v| | |
Wzoru na cosinus kąta nie pisze bo pewnie
bezendu zna i ten jest w tablicach
maturalnych .
5 sty 19:25