optymalizacja RS: Dane są punkty A = (1,5), B = (9,3) i prosta k o równaniu y = x+ 1 . Oblicz współrzędne punktu C leżącego na prostej k , dla którego suma |AC|²+|BC|² jest najmniejsza. Wyszła mi funkcja kwadratowa 4x²−32x+102

	32
wartość najmniejsza w wierzchołku xw=		=4
	8

y=5 C=(4,5) zgadzało by się

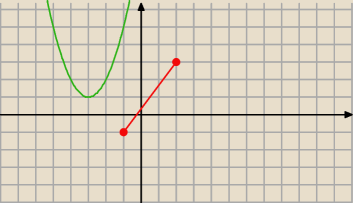
RS: Odcinek o końcach A(−2,−1) i B(2,3) jest podstawą trójkąta ABC Wierzchołek C należy do wykresu funkcji f(x)=x²+6x+10. Wyznacz współrzędne punktu C tak aby pole trójkąta ABC było najmniejsze Ile wynosi to pole Czy tutaj też chodzi o wierzchołek ? C=(−3,1) ?pole to sobie policzę ze wzoru, chodzi tylko o sprawdzenie mojego myślenia ?

RS: ?

Lorak: Nie chodzi o wierzchołek, kombinuj inaczej

RS: Zadanie za 6 punktów to chyba za proste jeśli by chodziło o wierzchołek odległość punktu od prostej AB ?

Lorak: