Kombinatoryka liceum klaudess: Bardzo proszę o pomoc 1.Na ile sposobów można wybrać 6 kart z talii 24 tak aby ; a. byly wsrod nich 3 piki LUB 3 kiery b. byly wsrod nich co najmniej 2 figury ( as, dama, krol, walet)? c. były wsrod nich karty ze wszystkich czterech kolorów? 2. Na ile sposobów osiem osób ; A,B,C,D,E,F,G,H może zająć miejsca przy okrągłym stole tak, aby osoby A i B siedziały na przeciwko siebie, jak również osoby C i D (na przeciwko siebie)?

Maslanek: a

	6 3		21 3
2*		*		−1

b od wszystkich możliwości odjąć te, które nie pasują c

6 1		6 1		6 1		6 1		20 2
	*		*		*		*

klaudess: a na 100 % dobrze? Mógłbyś wyjaśnić choć trochę ?

Maslanek: Biorę te 6 kart (kier, pik), wybieram z nich 3. Resztę 3 odkładam do kupki i z całej kupki biorę kolejne 3. Ale mogę mieć sytuacje, w której przypadkiem wylosuje trzy kiery i trzy piki. Te sytuacje należy odjąć Jeśli losuję z kierów i wyciągnę 3 piki − OK. Sytuacja ta już była teraz. Jeśli losuję z pików i wyciągnę 3 kiery − mam sytuację która była przed chwilą. Więc należy ją odrzucić.

klaudess: ehhh a pomyślisz nad drugim zadaniem, jak będziesz miał chwilę ? : >

Maslanek: Jak się wyśpię

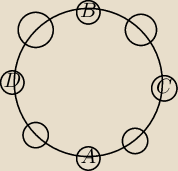
Rafał28: 2. Wszystko zależy od tego czy miejsca przy stole są ponumerowane czy też nie. Przypadek 1. Miejsca są ponumerowane. Wtedy A, B mogą zająć miejsca na 4 sposoby. Dla każdego takiego wyboru można te osoby wymieszać 2!. Nastepnie Osoby C, D w zależności od osób A, B mogą usiąść na 3 sposoby i też je można wymieszać na 2!. Pozostałe osoby można przestawiać dowolnie na 4! sposobów, czyli w sumie 4 * 2! * 3 * 2! * 4! = 1152 Przypadek 2. Miejsca nie są ponumerowane. Wtedy A, B mogą usiąść na jeden sposób. I dalej to samo w zależności od nich osoby C, D na 3 sposoby * 2! i pozostałe na 4! 3 * 2! * 4! = 144

klaudess: Bardzo, bardzo dziękuję! A w tym przypadku: Na ile sposobów osiem osób A,B,C,D,E,F,G,H może zająć miejsca przy okrągłym stole, tak aby osoby A i B siedziały obok siebie i osoby C i D również siedziały obok siebie? : /

klaudess: ej ej ej : D

Rafał28: Przypadek 1 (krzesła są ponumerowane) Osoby A, B zajmują miejsca na 8 sposobów * 2! bo mogą się zamieniać miejscami. Osoby C, D w zależności od osób A,B mogą zająć miejsca na 5 sposobów * 2!. Pozostałe osoby na 4!. 8 * 2! * 5 * 2! * 4! Przypadek 2 (krzesła nie są ponumerowane) Osoby A, B zajmują miejsca na 1 sposób. Osoby C, D na 5*2! sposobów. Pozostałe na 4!. 5 * 2! * 4!