Dla jakich wartości parametru bunia: dla jakich wartości parametru m (m∊R) zbiór rozwiazań nierówności x²+(m−1)x+m²≤0 zawiera się w zbiorze rozwiązań nierówności

x−1
	<0
x+1

ZKZ: Widze ze i gumisie sa na forum Kiedy rownanie kwadratowe ma rozwazania ? wtedy gdy delta >=0 A ta druga nierownoc to przeciez gumisie wiedza jak rozwiazac

bunia: niby to wiem ale cos mi ucieka Δ≥0 dla m∊<−1,1/3> druga nierówność to x ∊(−1,1) a jak to połączyć?

ZKZ: Skoro CI takie wyszly przedzialy to moze trzeba wyznaczyc czesc wspolna ? Ale moze jeszce ktos inny podpowie

bunia: tez tak zrobiłam (−1, ¹₃> ale się zastanawiam czy to jest dobrze?

Lorak: Nie, tak nie można

ZKZ: Wedlug mnie jest dobrze o ile dobrze wyznaczylas 1 przedzial (nie sprawdzalem)

bunia: coś za proste mi sie to wydaje

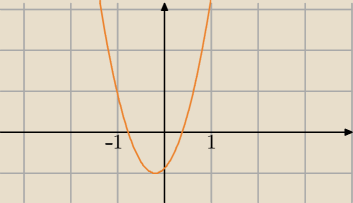
Lorak: Skoro zbiorem rozwiązań nierówności wymiernej jest x∊(−1,1), to teraz trzeba tak zrobić żeby zbiór rozwiązań nierówności kwadratowej zawierał się w tym zbiorze. Przykładowa sytuacja na rysunku. Spróbuj dobrać warunki.

bunia: no własnie z tymi warunkami mam problem

Lorak: Wartości dla x=−1 oraz dla x=1 muszą być większe od zera. Czyli rozwiązać f(−1)>0 i f(1)>0, f(x)=x²+(m−1)x+m²

bunia: z pierwszego warunku f(−1)>0 Δ<0 czyli brak rozwiązania z drugiego f(1)>0 Δ>0 m∊(−∞,−1)∪(0,∞) i to jest koniec?

Lorak: f(−1)>0, delta tak jak mówisz ujemna, czyli m∊R (parabola ponad osią iksów z ramionami w górę) f(1) jest ok. Teraz jeszcze musisz wyznaczyć część wspólną rozwiązań f(1)>0, f(−1)>0, Δ≥0 i to już będzie odpowiedź.