.
Piotr 10:
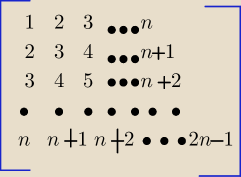
Oblicz sumę wszystkich liczb z tablicy:
Proszę o podpowiedź , zawsze mam z tymi tablicami problemy
3 sty 19:46
Saizou : zsumuj najpierw w wierszach a potem w kolumnach, albo na odwrót
3 sty 19:54
Piotr 10: S1=1+2+3+.....+n
S2=2+3+4+....+n+1
S3=3+4+5+....+n+2
.....
Sn=n+n+1+n+2+....+2n−1
I teraz do każdej sumy zastosować wzór na sumę skończonego ciągu arytmetycznego ?
3 sty 19:56
Saizou : dokładnie tak

3 sty 19:57
Piotr 10: Dobra coś mam
....
3 sty 20:03
Saizou : a ten skrajny prawy dolny to na pewno 2n−1

3 sty 20:12
Piotr 10: Yhym, tak mam na kartce. I coś nie pasuje, bo dalej nie wiem jak to zsumować
3 sty 20:14
Piotr 10: W sumie zadanie za 6 punktów
3 sty 20:19
Krzysiek: 1+2*2+3*3+...+n*n=∑k=1nk2
suma pod przekątną (z elementami 'n'):
(n−1)*(n+1)+(n−2)*(n+2)+...(n−(n−1))*(n+n−1)=∑k=1n−1(n−k)(n+k)=
=∑k=1n−1(n2−k2)=∑k=1n−1n2−∑k=1n−1k2
czyli całość to:
∑k=1nk2 +∑k=1n−1n2−∑k=1n−1k2 i teraz chyba łatwo policzysz?.
3 sty 20:25
Piotr 10: Krzysiek a możesz prościej napisać? Bo nie rozumiem Twojego zapisu
3 sty 20:27
PW: Sumy w kolumnach różnią się o n. W każdej następnej kolumnie wyrazy są powiększone o 1 w
stosunku do wyrazów poprzedniej kolumny
ak+1, m = ak, m + 1.
Wierszy jest n, a więc każda suma wyrazów w kolumnie następnej jest o n większa od
sumy wyrazów w kolumnie poprzedniej.
3 sty 20:29
Krzysiek: Piotr a orientujesz się w znaku sumy?
∑k=1nak=a1+a2+...+an
∑k=13k2=12+22+32
itd.
∑k=1nk2=∑k=1n−1k2+n2
pozostało policzyć: ∑k=1n−1n2=n2∑k=1n−11=...
3 sty 20:40
matyk: Skąd to zadanie? Zbyt trudne jak na maturę

3 sty 20:47
Panko: Patrz na przekątne (prawy górny−−−−−−lewy dolny) .
Weźmy n −−parzyste
Wtedy
Suma= 1*1 + 2*2+3*3 + (n−1)*(n−1) +n*n + (n+1)*(n−1)+(n+2*(n−2)+......(2n−2)*2+ (2n−1)*1=
1*(1+2n−1) + 2*(2+2n−2)+ 3*(3+2n−3)+.....(n−1)*( n−1+n+1) + n*n
1*2n +2*2n+3*3n+ ....+ (n−1)*2n +n2= 2n(1+2+3+....+ (n−1) ) +n2=
2n*(n−1)*( 1+ (n−1)) /2 +n2= 2n*(n−1)*n/2+n2=n2(n−1)+n2= n2*n=n3
Odp: Dla n −−−parzystych Suma wyrazów tablicy = n3
Teraz n−−nieparzyste ?
3 sty 21:53
PW: Jeszcze raz:
| | (n+1)n | |
− suma liczb z pierwszej kolumny jest równa 1+2+...+n = |
| = S1 |
| | 2 | |
− suma liczb z drugiej kolumny jest równa S
1+n = S
2
− suma liczb z trzeciej kolumny jest równa S
2+n i tak dalej.
Wszystkie liczby z tablicy zsumujemy obliczając sumę S
1+S
2+...+S
n − jako sumę ciągu
arytmetycznego, o różnicy n i liczbie wyrazów n.
Może to zadanie nie jest zbyt trudne na maturę rozszerzoną, tylko trzeba by zrezygnować z
idiotycznego pędzenia na czas (18 zadań na 180 minut).
3 sty 22:22
Piotr 10: Krzysiek niestety nie orientuję się w znaku sumy.
matyk to zadanie z arkuszy
maturalnych, które dostałem od pani ze szkoły. Czasami trudne zadania się tam zdarzają. Dzięki
za pomoc

4 sty 10:22
Piotr 10: Wyszła mi Suma całkowita tych wszystkich wyrazów Sc=n3
Zgadza się ?
4 sty 10:35
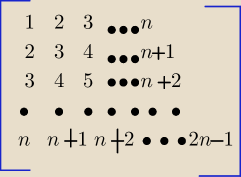 Oblicz sumę wszystkich liczb z tablicy:
Proszę o podpowiedź , zawsze mam z tymi tablicami problemy
Oblicz sumę wszystkich liczb z tablicy:
Proszę o podpowiedź , zawsze mam z tymi tablicami problemy



