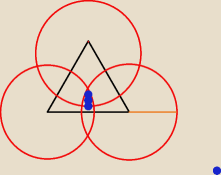
Środki trzech okręgów o promieniach równych 2 znajdują się w wierzchołkach trój ola: Środki trzech okręgów o promieniach równych 2 znajdują się w wierzchołkach trójkąta równobocznego o boku długości 2 √2 . Znaleźć pole części wspólnej tych trzech okręgów

ola:

ola: podpowie ktoś?

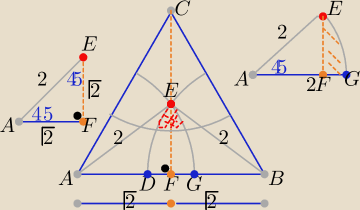
Eta: P(wycinka koła zawartego w tym trójkącie) o wierzchołku w A

	1		1		2
PwA=		πr2 =		π*4=		π
	6		6		3

F jest środkiem odcinka AB Trójkąt AFE jest równoramienny i prostokątny ( połówka kwadratu o boku √2 To P(FGE)( połówki "żelazka" : P= P(wycinka AGE)− P(ΔAFE)

	1		1		1
P=		πr2−		*(√2)2 =		π−1
	8		2		2

	1
To P(DGF)=2*(		π−1)= π−2
	2

Podobnie w wierzchołkach B i C Teraz : X −− pole szukanej części wspólnej: P(ΔABC) = 3P_wA −3P(żelazka) +X

	a2√3		2
to X =		−3*		π+3(π−2)=......... = 2√3+π−6 [j2]
	4		3

ola: a=2√2 h = √3/2 a h=√6 S trójkąta = 4√3 S okręgu = 4π .....?

ola: ok to trzeba wyliczyć z wycinka koła dzięki