punkty A (−2, 3) B (1, −2) Jan: punkty A (−2, 3) B (1, −2) są dwoma kolejnymi wierzchołkami rombu ABCD , a prostą o równaniu y=x+5 jest jego osią symetri wyznacz współrzędne wierzchołka CD .

Janek191: A = ( − 2; 3) B = ( 1; − 2) y = x + 5 − równanie osi symetrii rombu ABCD C = ( x; y) = ( x; x + 5) Musi być I AB I = I CB I √ (1 − (−2))² + ( − 2 −3)² = √ ( x − 1)² + ( x + 5 − (−2))² √ 9 + 25 = √ x² − 2x + 1 + x² + 14 x + 49 34 = 2 x² + 12 x + 50 2 x² + 12 x + 16 = 0 x² + 6 x + 8 = 0 ( x + 4)*( x + 2) = 0 x = − 4 lub x = − 2 więc y = 1 lub x = 3 C = ( − 4; 1) lub C = ( − 2; 3) = A − odpada ========= Punkt D jest symetryczny do punktu B oraz I AD I = I CD I Niech D = ( a; b) √ ( a + 2)² + ( b −3)² = √ ( a + 4)² + ( b − 1)² √ a² + 4 a + 4 + b² − 6 b + 9 = √ a² + 8 a + 16 + b² − 2 b + 1 a² + 4a + b² − 6 b + 13 = a² + 8 a + b² − 2b + 17 4a − 6b + 13 = 8a − 2b + 17 4a + 4b = − 4 a + b = − 1 ⇒ b = − a − 1 D = ( a; − a − 1) I AD I = I AB I = √34 √( a + 2)² + ( − a − 4)² = √34 √ a² + 4a + 4 + a² + 8 a + 16 = √34 2a² + 12a + 20 = 34 2 a² + 12 a − 14 = 0 a² + 6a − 7 = 0 ( a + 7)*( a − 1) = 0 a = − 7 lub a = 1 więc b = 6 lub b = 0 D = ( − 7; 6) −−−−−−−− Odp. C = ( − 4; 1) , D = ( − 7; 6) =============================

Janek191: II sposób: C = ( − 4; 1) obliczone jak w I sposobie. D = ( a; b) → → AD = BC [ a + 2; b − 3 ] = [ − 5; 3 ] a + 2 = − 5 i b − 3 = 3 a = − 7 i b = 6 D = ( − 7 ; 6 ) ===========

ZKZ: I jeszce do pelni szczescia Janek191 dla Jana powinien zrobic rysunek i max ilosc punktpw za zadanie jest

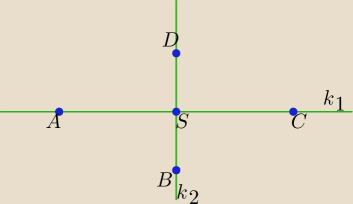
Bogdan: Proponuję takie rozwiązanie: k₁: y = x+5, a₁ = 1 i A(−2, 3)∊k₁ k₂: y = a₂x+b₂ i B(1, −2)∊k₂, k₂⊥k₁ ⇒ a₂ = −1 i y = −(x −1) −2 ⇒ y = −x−1 S = k₁∩k₂ ⇒ x + 5 = −x − 1 ⇒ x = −3 i y = −3 + 5 = 2 ⇒ S = (−3, 2) C(x_c, y_c): x_c − 2 = 2*(−3) ⇒ x_c = −4, y_c + 3 = 2*2 ⇒ y_c = 1, D(x_D, y_D): y_D + 1 = 2*(−3) ⇒ x_D + 1 = 2*(−3) ⇒ x_D = −7, y_D −2 = 2*2 ⇒ y_D = 6, C(−4, 1), D(−7, 6)