 1. Przez punkt styczności s dwóch okręgów O1 i O2 prowadzimy dwie proste: prostą k która
przecina O1 w punkcie A i O2 w punkcie B oraz prostą l która przecina O1 w punkcie i O2 w
punkcie D. Udowodnij, że AC ∥ BD.
2. W okręgu rysujemy średnicę AB i równoległą do niej cięciwę CD. Udowodnij, że różnica miar
kątów ACD i CDA jest równa 90 stopni.
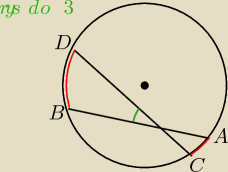
3. Cięciwy AB i CD przecinają się pod kątem 36 stopni. Wyznacz kąty środkowe odpowiadające
łukom AC i BD, jeżeli ich stosunek wynosi 1 : 3.
1. Przez punkt styczności s dwóch okręgów O1 i O2 prowadzimy dwie proste: prostą k która
przecina O1 w punkcie A i O2 w punkcie B oraz prostą l która przecina O1 w punkcie i O2 w
punkcie D. Udowodnij, że AC ∥ BD.
2. W okręgu rysujemy średnicę AB i równoległą do niej cięciwę CD. Udowodnij, że różnica miar
kątów ACD i CDA jest równa 90 stopni.
3. Cięciwy AB i CD przecinają się pod kątem 36 stopni. Wyznacz kąty środkowe odpowiadające
łukom AC i BD, jeżeli ich stosunek wynosi 1 : 3.


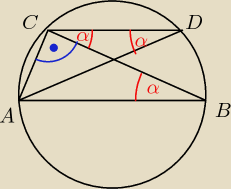 kąty ADC i ABC oparte na tym samym łuku, kąty ABC i BCD naprzemianległe przy prostych
równoległych, kąt ACB prosty bo oparty na półokręgu.
kąty ADC i ABC oparte na tym samym łuku, kąty ABC i BCD naprzemianległe przy prostych
równoległych, kąt ACB prosty bo oparty na półokręgu.
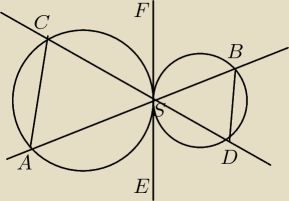 Skorzystam z twierdzenia: kąt między styczną a cięciwą jest równy kątowi wpisanemu opartemu na
tej cięciwie.
Prosta EF jest wspólną styczną tych okręgów.
|<FSB|=|<ASE| − wierzchołkowe
|<FSB|=|<SDB| − z tego twierdzenia
|<ASE|=|<ACS| − też z tego twierdzenia
więc |<ACS|=|<SDB|, a są to kąty naprzemianległe przy prostych AC i BD, więc proste te są
równoległe.
Skorzystam z twierdzenia: kąt między styczną a cięciwą jest równy kątowi wpisanemu opartemu na
tej cięciwie.
Prosta EF jest wspólną styczną tych okręgów.
|<FSB|=|<ASE| − wierzchołkowe
|<FSB|=|<SDB| − z tego twierdzenia
|<ASE|=|<ACS| − też z tego twierdzenia
więc |<ACS|=|<SDB|, a są to kąty naprzemianległe przy prostych AC i BD, więc proste te są
równoległe.
| r2 | ||
skali k = − | . W tej jednokładności obrazem odcinka AC jest odcinek BD, a odcinki | |
| r1 |
 co do 3. nie wiem, jakie kąty mam obliczyć
co do 3. nie wiem, jakie kąty mam obliczyć
 dzięki
dzięki