Rachunki różniczkowe - zadania tekstowe. nieumiem: Jakie powinny być wymiary słoika w kształcie walca o grubości ścianek d=3mm i pojemności V=0,5dm³, aby ilość szkła potrzebna do jego wytworzenia była najmniejsza? Nie wiem jak się za to zabrać.

nieumiem: up

nieumiem: up

daras: odejmij od objętości większego walca, objętość mniejszego i ci wyjdzie

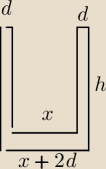
AS: Dane: d = 3 mm = 0.03 dcm , V = 0.5 dcm³ Objętość naczynia: V = π*(x + 2*d)²*h/4 − π*x²*(h − d)/4 V = π/4*[(x + 2*d)²*h − x²*(h − d)] V = π/4[x²*h + 4*x*d*h + 4*d²*h − x²*h + x²*d] V = π/4*[4*x*d*h + 4*d²*h + x²*d] 4*x*d*h + 4*d²*h + x²*d = 4*V/π = p gdzie p = 4*V/π

	p − x2*d		1		p − x2*d
h =		=		*
	4*d*(x + d)		4*d		x + d

Obliczam pochodną h

	−2*x*d*(x + d) − (p − x2*d)*1
h' =
	(x + d)2

Po uporządkowaniu licznika x²*d + 2*x*d + p = 0 Rozwiązując równanie kwadratowe znajdziemy x dla minimum

nieumiem: dzięki~!