Funkcja kwadratowa EMPE: Dane jest równanie |x² + 2x − 8| = 5m − 25 z niewiadomą x. Wyznacz zbiór wszystkich wartości parametru m (m ∊ R), dla których równanie ma 4 różne rozwiązania, w tym dokładnie 2 ujemne.

	3
Odpowiedź to m ∊ ( 5, 6		〉
	5

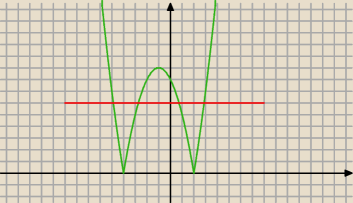
Aga1.: Narysuj wykres y=Ix²+2x−8I kolor czerwony i y=5m−25 dla różnych m

	−b
p=		=−1
	2a

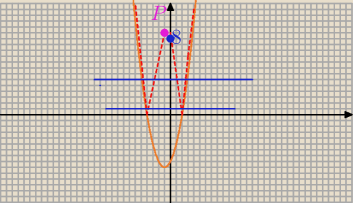
q=f(−1)=1−2−8=−9 P=(p,IqI)=(−1,9) Prosta o równaniu y=2m−25 ma z wykresem 4 punkty wspólne (4 rozwiązania i 2 ujemne)gdy 5m−25>0 i 5y−25≤8 Rozwiąż te nierówności i wyznacz część wspólną.

Bizon: