ciag aryt cincin: Zbadaj monotoniczność ciągu określonego wzorem: an=n²+3n wg mnie nie jest monotoniczny, ale odp: rosnący

dana: policz wyraz a_n+1 czyli wstaw za n liczbę (n+1), a następnie oblicz różnicę a_n+1 −a_n i jak otrzymasz =0 to stały, jak liczbe ujemna to malejący a jak dodatnia to rosnący . pamiętaj że n jest naturalną liczbą. powodzenia

Radek: a_n+1=(n+1)²+3(n+1) a_n+1=n²+2n+1+3n+3 a_n+1=n²+5n+4 a_n+1−a_n= =n²+3n−(n²+5n+4) =n²+3n−n²−5n−4 =−2n−4=−2(n−2) więc ?

cincin: dlaczego zatem ciag an=(n−3)² nie jest monotoniczny?

cincin: ?

5-latek: Aby stwierdzic czy dany ciag a_n jest ciagiem momotonicznym to nalezy zbadac roznice

	an+1
an+1−an lub iloraz
	an

Najpierw mozesz wypisac sobie kilka poczatkowych wyrazow tego ciagu i zobaczysz jaki ten ciag moze byc . jednak ostateczne okreslenie jaki ten ciag jest to zbadanie albo tej roznicy albo tego ilorazu

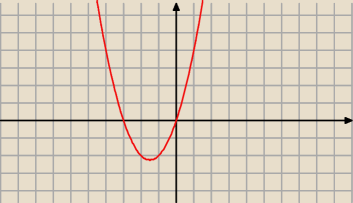
Gustlik: Można funkcją − to funkcja kwadratowa: a_n=n²+3n y=x²+3x Liczę wierzchołek paraboli:

	b		3
p=−		=−		, czyli jest na minusie.
	2a		2

a>0 czyli ramiona w dół. A więc po dodatniej półosi OX, gdzie znajdują się liczby naturalne (dziedzina ciągu) funkcja rośnie, czyli ciąg też rośnie − patrz wykres. Metoda "na funkcję" jest prostsza niż liczenie a_n+1−a_n i dla ciągów danych wzorami łatwych do zbadania funkcji (liniowa, kwadratowa, homograficzna, wykładnicza i logarytmiczna) jest ona łatwiejsza, choć tę "szkolną" też trzeba znać, bo nie poradzimy sobie przy ciagach np. wielomianowych, wymiernych bardziej skomplikowanych niż homograficzne, czy przy ciągach typu a_n=n! itd...

5-latek: Gustlik Malenkie sprostowanie a>0 ramiona w gore