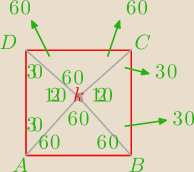
l Radek: Punkt K należący do wnętrza kwadratu połączono odcinkami z wierzchołkami kwadratu.Oblicz kąty trójkąta ABK wiedząc, że CDK jest równoboczny. W odpowiedzi jest inaczej ?

Radek: ?

Radek: ?

.: Zły rysunek. Narysuj sobie na kratkach papieru jak będzie to wyglądało. Dokładnie. Dwa trójkąty równoboczne nie zmieścisz w ten sposób.

ciekawsky: 120,30,30 powinno być

pigor: ... , np. tak : musisz zauważyć, że jeśli ΔCDK − równoboczny, to ΔABK wcale taki nie jest tylko kolejno np. tak : w ΔADK (180^o−30^o) : 2= 75^o ⇒ 90^o−75^o= 15^o= |∡KAB|= |∡KBA) , zatem |∡AKB|= 180^o−2*15^o= 150^o i to tyle . ...

Radek:

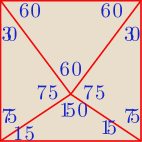
Radek: Po narysowaniu i zmierzeniu linijką stwierdziłem że te dwa trójkąty po bokach są równoramienne ale jak to wykazać bez rysowania (zauważyć) ?

Radek: już wiem

Eta:

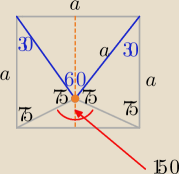
Radek: Wyszło mi tak samo jak Pani a czy te kąty 75 przy k to katy wierzchołkowe ?

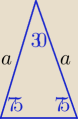
Eta: Nie ... to są kąty przy podstawie trójkąta równoramiennego

Radek: Czyli jak bez mierzenia linijką wykazać że ten trójkąt z boku jest równoramienny ?

.: Trójkąt równoramienny to taki, który ma dwa boki równej długości. W tym przypadku długości a.

Eta: trójkąty AKD i BKC mają ramiona "a" i kąt między tymi ramionami 90^o−60^o= 30^o bo trójkąt CDK jest równoboczny o boku "a"

pigor: ..., . dziękuję Panie Radku .

Eta: dla Pana pigora

Radek: Dziękuję Panie pigorze !

Eta:

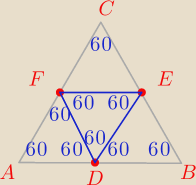
Radek: Na nokach trójkąta AB, BC i AC trójkąta równobocznego ABC wybieramy odpowiednio taki punkty D,E i F tak,że AD=BE=CF udowodnij, że trójkąt DEF jest równoboczny Ale jak to ładnie wykazać ? Na rysunku wszystko ładnie widać

.: Udowodnij, że trójkąty ADF, BED, CFE są przystające.

Radek: Dzięki