Geometria analityczna. Magda: Napisz równanie okręgu: a) przechodzącego przez punkt P=(1,0) i stycznego do prostych określonych równaniami x+y−2=0 oraz x+y+3=0 b) o promieniu 3, który jest styczny do osi y i prostej o równaniu x+y=0 Proszę o jakąkolwiek pomoc.

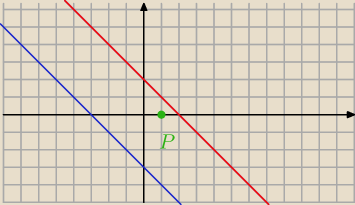
bezendu: Widzisz już ?

Magda: Nie bardzo

bezendu: Kolejna wskazówka: odległość punktu od prostej.

5-latek:

	|C2−C1|
Jest wzor na odlegolosc miedzy prostymi d=
	√A2+B2

Polowa odleglosci to promien tego okregu Teraz sie zastanow jakie bedzie rownanie prostej na ktorej bedzie lezal ten srodek ? To byla wskazowka do zadania nr 1

Magda:

	5 √2		25
obliczyłam i wyszło		czyli r2=
	2		8

5-latek: Poprawiam chochlika Tam we wzorze na d w liczniku ma byc |C−1−C−2| .

5-latek: I znowu chochlik . czes przestac pisac ma byc oczywiscie |C₁−C₂| Teraza OK

Magda: może ktoś podpowiedzieć z tym rownaniem prostej na ktorej lezy srodek?

Magda: Proszę bardzo zależy mi na tym zadaniu.