jak rozwiązać Konrad: Jak rozwiązać : (x−1)(2x²+2x−4)≥0

Konrad: Proszę o pomoc : |x³−6x²+9x−4|>x³−6x²+9x−4

bezendu: 2(x−1)(x²+x−2)≥0 / :2 (x−1)(x²+x−2)≥0 w nawiasie policz Δ

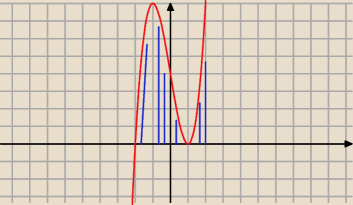
Aga1.: Obliczasz miejsca zerowe przyrównując każdy nawias do 0. Rysujesz wężyk od góry z prawej strony uwzględniając krotność pierwiastków. Zapisujesz odp.

Konrad: Czyli odpowiedź wychodzi x∊<−2,∞) ?

Aga1.: Tak.

Konrad: Dziękuje zastanawiam się jeszcze nad tym : |x3−6x2+9x−4|>x3−6x2+9x−4

Kaja: rozwiąż to sobie w odpowiednich przedziałach. zauważ, że x³−6x²+9x−4=(x−1)(x−3)(x−4) sprawdź dal jakich x (x−1)(x−3)(x−4)≥0, a dla jakich (x−1)(x−3)(x−4)<0.

pigor: ..., np. tak : 1. (x−1)(2x²+2x−4) ≥0 ⇔ (x−1) (2x²−2x+4x−4) ≥0 ⇔ ⇔ (x−1) (2x(x−1)+4(x−1))= 0 ⇔ (x−1)(x−1) (2x+4)= 0 ⇔ (x−1)²*2 (x+2)= 0 ⇔ ⇔ x−1=0 v x+2=0 ⇔ x=1 v x= −2 ⇔ x∊{1,−2} − szukane rozwiązanie, przy czym x=1 − pierwiastek dwukrotny (krotności 2) . ...

pigor: .. o kurcze, przepraszam, to jest nierówność , więc (x−1)²(x+2) ≥ 0 ⇔ x ≥ −2 ⇔ x∊[−2;+∞) .

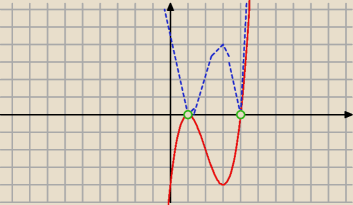
Aga1.: Metoda graficzna f(x)=Ix³−6x²+9x−4I kolor niebieski g(x)=x³−bx²+9x−4 kolor czerwony Odp x≠1 i x≠4

Konrad: Aga1 odpowiedź chyba powinna wyjść x∊(−∞,4) −{1} jeśli się pomyliłem to popraw mnie.