Planimetria
Radek:
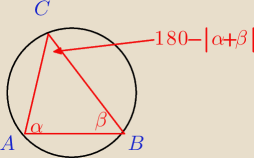
Dwa kąty trójkąta wpisanego w okrąg o promieniu R mają miary α i β. Znajdź pole tego trójkąta i
długość promienia okręgu wpisanego w ten trójkąt.
|| to oznacza nawias.
|AC|=sinβR
|AB|=sin(α+β)R
P=0,5*sinβR*sin(α+β)R*sinα
P=0,5sinβsinαsin(α+β)R
2
Czy ta część zadania jest poprawnie zrobiona ?
1 sty 19:18
Hajtowy: Naturlish
1 sty 19:24
Mila:
Popraw konsekwentnie i będzie dobrze.
1 sty 19:27
Radek:
Druga cześć zadnia.
|BC|=sinαR
| | 0,5sinβsinαsin(α+β)R2 | |
r= |
| |
| | sinβR+sin(α+β)R+sinαR | |
| | 0,5sinβsinαsin(α+β)R2 | |
r= |
| |
| | R(sinβ+sin(α+β)+sinα | |
| | 0,5sinβsinαsin(α+β)R | |
r= |
| |
| | sinβ+sin(α+β)+sinα | |
?
1 sty 19:29
Radek:
Pomyliłem wzór, przepraszam. Ale jeśli poprawię 2R to też będzie ok ?
1 sty 19:31
Mila:
Popraw korzystanie z tw. sinusów.
1 sty 19:35
Radek:
|AC|=sinβ2R
|AB|=sin(α+β)2R
|CB|=sinβ2R
P=0,5*sinβ2R*sin(α+β)2R
P=sinβsin(α+β)2R
2
| | sinβsin(α+β)2R2 | |
r= |
| |
| | 2R(sinβ+sin(α+β)+sinα) | |
| | sinβsin(α+β)R | |
r= |
| |
| | sinβ+sin(α+β)+sinα | |
Teraz dobrze ?
1 sty 19:41
Radek:
Coś z tym r chyba nie pasuję ?
1 sty 19:48
5-latek: Ja nie sprwdzalem bo to nie na moje mozliwosci dzisiaj ale z jakiego wzoru skorzystales
obliczajac r
czy z tego P=p*r gdzie p to polowa obwodu maz ztwego co widze P policzone boki policzne to
wyznacz r
1 sty 19:52
Radek:
Już wyznaczyłem r. Ale chodzi o to czy jest to poprawnie ?
1 sty 19:53
5-latek: | | 2P | |
czy z tego r= |
| ? |
| | AB+BC+AC | |
1 sty 19:54
Radek:
Tak.
1 sty 19:55
Mila:
Masz pomyłkę :
|CB|=2Rsinα
sin(180−(α+β))=sin(α+β)
| | 1 | |
PΔ= |
| *2Rsinβ*2Rsin(α+β)*sinα |
| | 2 | |
a+b+c=2R*sinα+2R*sinβ+2R*sin(α+β)
a+b+c=2R(sinα+sinβ+sin(α+β))
Teraz dokończ i zwróć uwagę na zapisy.
1 sty 19:55
Radek:
Pole wychodzi:
P=2R
2sinβsinαsin(α+β) i tutaj zgadza teraz się z odpowiedziami
| | 4R2sinβsinαsin(α+β) | |
r= |
| |
| | 2R(sinα+sinβ+sin(α+β) | |
| | 2Rsinβsinαsin(α+β) | |
r= |
| |
| | sinα+sinβ+sin(α+β) | |
Dziękuję, już znalazłem błąd.
1 sty 20:01
Radek:
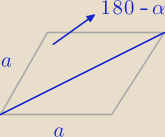
Dłuższa przekątna rombu, którego kąt ostry ma miarę α, ma długość p. Znajdź promień okręgu
wpisanego w ten romb.
cos(180−α)=−cosα
p
2=a
2+a
2−[2a
2*(−cosα)]
p
2=2a
2+2a
2cosα
p
2=2a
2(1+cosα)
p=a
√2(1+cosα)
P=a
2
?
1 sty 20:20
Radek: ?
1 sty 20:33
Eta:
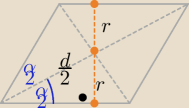
| | α | |
sin |
| =....... ⇒ r=........... |
| | 2 | |
1 sty 20:44
Radek:
A co jest nie poprawnie w moim rozwiązaniu ? Proszę o wskazanie błędów.
1 sty 20:45
Eta:
| | p | | d | |
zamiast |
| napisałam przez nieuwagę |
| |
| | 2 | | 2 | |
1 sty 20:45
Eta:
Masz dane : α i p
odp nie może zawierać "a"
1 sty 20:46
1 sty 20:49
Radek:
Czyli w mianowniku zamiast 4a powinno być U{4p}{√2(1+cosα) ?
1 sty 20:51
Mila:
W Twoim rozwiązaniu masz błędny wzór na pole rombu;
Prombu=a2*sinα
1 sty 20:54
Radek:

Racja, dziękuję.
Oblicz pole równoległoboku o kącie ostrym α i przekątnych p i q (p>q)
Tutaj nie mam pomysłu na to zadanie ?
1 sty 20:56
Aga1.: P=a*b*sinα, gdzie a i b to boki równoległoboku
a * b wyliczysz z układu równań stosując dwa razy tw. cosinusów
q2=a2+b2−2*a*b*cosα
p2=a2+b2−2*a*b*cos(1800−α)
1 sty 21:02
Eta:
Poprzednie zadanie można jeszcze dokończyć
| | α | | α | | α | |
sinα= 2sin |
| *cos |
| i 1+cosα= 2cos2 |
| |
| | 2 | | 2 | | 2 | |
| | p | | α | |
i teraz widać,że r= ...... = |
| *sin |
| |
| | 2 | | 2 | |
czyli taka odp jaką podałam w poprzednim poście
1 sty 21:03
Mila:
P=a*b*sinα
Pisz tw. cosinusów, zobacz czy możesz obliczyc a*b.
1 sty 21:03
Radek:
Czyli z twierdzenia cosinusów.
b2=0,5p*0,5q−(2*0,5p*0,5qcosγ) dobrze myślę ?
1 sty 21:09
Eta:
Widzę,że masz pomoc ze strony Mili , więc nie przeszkadzam

1 sty 21:10
Radek:
Pani pomoc też jest mi bardzo potrzebna !
1 sty 21:10
Radek: ?
1 sty 21:16
Kejt: całe forum chcesz ściągnąć do pomocy?

1 sty 21:17
Mila:
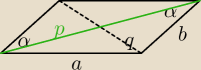
Nie !
α− kat ostry
p
2=a
2+b
2−2ab*(−cosα)
q
2=a
2+b
2−2ab*cosα dodaję stronami
p
2+q
2=a
2+b
2
Podstaw do I równania,...oblicz potem (ab) i gotowe.
1 sty 21:20
Eta:
Ejj
Mila 
p
2+q
2=
2(a
2+b
2)
1 sty 21:22
Radek:
a no tak α to kąt ostry a nie kąt przecięcia się przekątnych.
1 sty 21:23
1 sty 21:28
Mila:
No właśnie, trzeba iść spać, bo źle liczę, dziękuję za poprawkę.

Dobrze Radek.
1 sty 21:29
Radek:
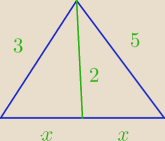
Dwa boki trójkąta mają długość 3 i 5 a środkowa poprowadzona do trzeciego boku ma długość 2.
Oblicz długość trzeciego boku.
2x
2=5
2+3
2−(2*5*3cosα)
x
2=2
2+5
2−(2*2*5*cosα)
x
2=3
2+2
2−(2*2*3*cosα)
układ równań ?
1 sty 21:32
Mila:
Co z tym kątem, wszędzie α?
1 sty 21:35
Radek:

Czyli jak to powinno wyglądać ?
1 sty 21:36
Eta:
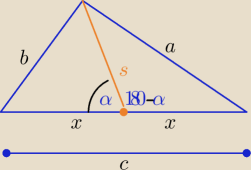
1 sty 21:40
1 sty 21:42
Radek:
cos(180−α)=−cosα
b2=x2+s2−2xscosα
a2=s2+x2+2sccosα
?
1 sty 21:43
Aga1.: Wystarczy układ 2 równań. Kąt α między bokami 3 i 2x.
52=32+4x2−2*3*2x*cosα , w dużym trójkącie.
22=32+x2−2*3x*cosα, w małym trójkącie z lewej strony
1 sty 21:44
Radek:
Pani Eto z tego wzoru można policzyć c tak ? chodzi o ten wzór w wikipedii ?
1 sty 21:46
Eta:
tak

( możesz go zawsze wyprowadzić z tw. kosinusów)
1 sty 21:52
Radek:
d=0,5p{2a2+2b2−c2) /2
d2=0,25(2a2+2b2−c2)
4=0,25(2*32+2*52−c2)
4=0,25(18+50−c2)
4=17−0,25c2
−0,25c2=−13 / *(−1)
0,25c2=13
c2=52
c=2√13
A muszę to koniecznie wyprowadzać ? Nie mogę od razu z tego skorzystać ?
1 sty 21:55
Eta:
Możesz , jeżeli go zapamiętasz i podasz na maturze ,że z takiego wzoru korzystasz

1 sty 21:58
Radek:
Zapamiętam.
Wykaż, że w trójkącie ostrokątnym o bokach różnej długości naprzeciwko najdłuższego boku leży
kat o najmniejszej mierze.
a−najdłuższy bok
b −bok średniej długości
c−najkrótszy bok
| c | | b | |
| = |
| itp ? czy nie ? |
| sinγ | | sinβ | |
1 sty 22:06
Aga1.: Sprawdź treść zadania, bo podane zdanie jest fałszywe.
1 sty 22:11
Radek: o największej mierze.
1 sty 22:12
Radek: ?
1 sty 22:22
Eta:
Jeżeli α≤β≤γ i α,β,γ∊(0o,90o) to a≤b≤c
a=2R*sinα, b=2R*sinβ, c= 2R*sinγ
to.....
1 sty 22:35
Radek:
Twierdzenie sinusów mam ?
1 sty 22:36
Radek: ?
1 sty 22:45
Eta:
Jeszcze nie wiesz?
1 sty 22:50
Radek:
Nie wiem dalej, do tego też doszedłem ale co to daję ?
1 sty 22:53
Eta:
Jeżeli α≤β≤γ ⇒ sinα≤sinβ≤sinγ i R −− stałe
zatem a≤b≤c
c.n.u

1 sty 22:55
Radek: To tyle tylko ?

Dziękuję
1 sty 22:57
Eta:
No tyle

1 sty 22:58
Radek:
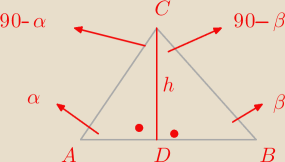
W trójkącie ABC mamy dane wysokość |CD|=h |∠BAC|=α i |∠ABC|=β oblicz pole tego trójkąta
a) ostrokątnego β
|AC|sinα=h
|CB|sinβ=h
|∠ACB|=90−α+90−β=180−(α+β)
sin[180−(α+β)]=sin(α+β)
| | h | | h | |
P=0,5* |
| * |
| *sin(α+β} |
| | sinβ | | sinβ | |
| | h2sin(α+β) | |
P=0,5* |
| |
| | sinαsinβ | |
?
1 sty 23:11
Eta:
ok

| | h | | h | | 1 | | 1 | |
2 sposób |AD|= |
| , |DB|= |
| , P= 0,5h2( |
| + |
| ) [j2] |
| | tgα | | tgβ | | tgα | | tgβ | |
1 sty 23:20
Radek:
Mogę jeszcze liczyć na Pani pomoc ?
1 sty 23:23
Eta:
Oczywiście wynik jest taki sam jak u Ciebie

| | sin(α+β) | |
bo tgα+tgβ= |
| |
| | cosα*cosβ | |
| | sin(α+β) | |
co daje że P= 0,5h2* |
| j2 |
| | sinα*sinβ | |
1 sty 23:24
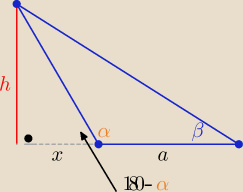
Radek:
To samo polecenie : obliczyć pole ale kąt BAC jest rozwarty ?
1 sty 23:27
Radek: ?
1 sty 23:39
bezendu:

1 sty 23:49
Radek: ?
2 sty 00:00
Radek: pomoze ktoś ?
2 sty 00:10
Eta:
Wystarczy ?
2 sty 00:18
Radek: Tak.
2 sty 00:19
Radek:
Dziękuję za pomoc.

2 sty 00:20
Eta:
Tylko pamiętaj,że 180
o−α −−− jest kątem ostrym

2 sty 00:22
Radek:
Dobrze, jutro albo w piątek będę jeszcze więcej zadań wstawiał nie koniecznie do rozwiązania.
Dobranoc

2 sty 00:26
Eta:
Miłych snów

2 sty 00:27
Radek:
Czy zauważyła Pani poprawę w mojej planimetrii ?
2 sty 00:28
Eta:
Jasne,że tak

.., tylko trochę więcej wiary w siebie,
bo na maturze nie będzie kogo zapytać o poprawny wynik

Jeszcze jest sporo czasu, rozwiązując zadania nabierzesz wprawy i będzie ok

A o tej porze .... to już powinieneś smacznie spać( umysł wypoczęty, to połowa sukcesu)
Dobrej nocy

2 sty 00:34
Radek:
Dziękuję za odpowiedź. Dobrej nocy.
2 sty 00:36
5-latek: Wracajac do zadania gdzie miales wykazac ze naprzeciw najwiekszsego boku lezy najwiekszy kat
to do wykaznia mozna tez bylo skorzystac z wlasnosci kata zewnetrzrnego trojkata
2 sty 11:38
 Dwa kąty trójkąta wpisanego w okrąg o promieniu R mają miary α i β. Znajdź pole tego trójkąta i
długość promienia okręgu wpisanego w ten trójkąt.
|| to oznacza nawias.
Dwa kąty trójkąta wpisanego w okrąg o promieniu R mają miary α i β. Znajdź pole tego trójkąta i
długość promienia okręgu wpisanego w ten trójkąt.
|| to oznacza nawias.
 Dłuższa przekątna rombu, którego kąt ostry ma miarę α, ma długość p. Znajdź promień okręgu
wpisanego w ten romb.
cos(180−α)=−cosα
p2=a2+a2−[2a2*(−cosα)]
p2=2a2+2a2cosα
p2=2a2(1+cosα)
p=a√2(1+cosα)
Dłuższa przekątna rombu, którego kąt ostry ma miarę α, ma długość p. Znajdź promień okręgu
wpisanego w ten romb.
cos(180−α)=−cosα
p2=a2+a2−[2a2*(−cosα)]
p2=2a2+2a2cosα
p2=2a2(1+cosα)
p=a√2(1+cosα)

 Racja, dziękuję.
Oblicz pole równoległoboku o kącie ostrym α i przekątnych p i q (p>q)
Tutaj nie mam pomysłu na to zadanie ?
Racja, dziękuję.
Oblicz pole równoległoboku o kącie ostrym α i przekątnych p i q (p>q)
Tutaj nie mam pomysłu na to zadanie ?


 Nie !
α− kat ostry
p2=a2+b2−2ab*(−cosα)
q2=a2+b2−2ab*cosα dodaję stronami
p2+q2=a2+b2
Podstaw do I równania,...oblicz potem (ab) i gotowe.
Nie !
α− kat ostry
p2=a2+b2−2ab*(−cosα)
q2=a2+b2−2ab*cosα dodaję stronami
p2+q2=a2+b2
Podstaw do I równania,...oblicz potem (ab) i gotowe.
 p2+q2= 2(a2+b2)
p2+q2= 2(a2+b2)
 Dobrze Radek.
Dobrze Radek.
 Dwa boki trójkąta mają długość 3 i 5 a środkowa poprowadzona do trzeciego boku ma długość 2.
Oblicz długość trzeciego boku.
2x2=52+32−(2*5*3cosα)
x2=22+52−(2*2*5*cosα)
x2=32+22−(2*2*3*cosα)
układ równań ?
Dwa boki trójkąta mają długość 3 i 5 a środkowa poprowadzona do trzeciego boku ma długość 2.
Oblicz długość trzeciego boku.
2x2=52+32−(2*5*3cosα)
x2=22+52−(2*2*5*cosα)
x2=32+22−(2*2*3*cosα)
układ równań ?
 Czyli jak to powinno wyglądać ?
Czyli jak to powinno wyglądać ?

 ( możesz go zawsze wyprowadzić z tw. kosinusów)
( możesz go zawsze wyprowadzić z tw. kosinusów)

 Zapamiętam.
Wykaż, że w trójkącie ostrokątnym o bokach różnej długości naprzeciwko najdłuższego boku leży
kat o najmniejszej mierze.
a−najdłuższy bok
b −bok średniej długości
c−najkrótszy bok
Zapamiętam.
Wykaż, że w trójkącie ostrokątnym o bokach różnej długości naprzeciwko najdłuższego boku leży
kat o najmniejszej mierze.
a−najdłuższy bok
b −bok średniej długości
c−najkrótszy bok

 Dziękuję
Dziękuję

 W trójkącie ABC mamy dane wysokość |CD|=h |∠BAC|=α i |∠ABC|=β oblicz pole tego trójkąta
a) ostrokątnego β
W trójkącie ABC mamy dane wysokość |CD|=h |∠BAC|=α i |∠ABC|=β oblicz pole tego trójkąta
a) ostrokątnego β



 Wystarczy ?
Wystarczy ?




 .., tylko trochę więcej wiary w siebie,
bo na maturze nie będzie kogo zapytać o poprawny wynik
.., tylko trochę więcej wiary w siebie,
bo na maturze nie będzie kogo zapytać o poprawny wynik  Jeszcze jest sporo czasu, rozwiązując zadania nabierzesz wprawy i będzie ok
Jeszcze jest sporo czasu, rozwiązując zadania nabierzesz wprawy i będzie ok A o tej porze .... to już powinieneś smacznie spać( umysł wypoczęty, to połowa sukcesu)
Dobrej nocy
A o tej porze .... to już powinieneś smacznie spać( umysł wypoczęty, to połowa sukcesu)
Dobrej nocy 