Wykaż zalezność w trapiezie równoramiennym. Kaki: Trapez równoramienny ABCD o podstawach AB i CD jest opisany na okręgu o promieniu r. Wykaż, że 4r² = |AB|*|CD. Zadanie z matury rozszerzonej z 2013 roku z maja. Wiem jak je zrobić ale zastanawia mnie czy korzystając z tego, że |AB|, 2r, |CD| − jest ciągiem geometrycznym |AB|, r, |CD| − jest ciągiem arytmetycznym można też jakoś udowodnić tę zależność?

+-: Wskazówki: Zrób rysunek. Ramiona kąta opisanego na okręgu są równe. Pitagoras

Kaki: * |AB|, 2r, |CD| − jest ciągiem arytmetycznym Wiem jak zrobić to zadanie. Ale zastanawiam się czy z tych zależności też można je rozwiązać.

+-: A na jakiej podstawie twierdzisz: |AB|, 2r, |CD| − jest ciągiem arytmetycznym

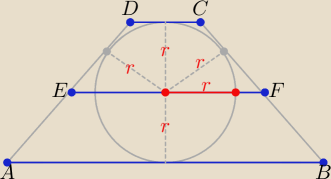
Bogdan: Długości odcinków: AB, EF, CD tworzą ciąg arytmetyczny.

	|AB| + |CD|
|EF| =
	2

Kaki: Za krzywe te rysunki maluje W czym je robisz? Coś kiedyś słyszałem, że przy logarytmowaniu wyrazów (dodatnich) ciągu geometrycznego otrzymujemy ciąg arytmetyczny. Mógłbyś to rozwinąć (tzn jak to zapisać?)

Bogdan: Klikam przycisk rysuję i wykorzystuję znajdujące się tam narzędzia do rysowania. To logarytmy przy podstawie np. c kolejnych wyrazów ciągu geometrycznego o ilorazie q tworzą ciąg arytmetyczny. Stała różnica takiego ciągu arytmetycznego jest równa log_c q.