Dla jakich wartości parametru k, równanie (k-2)x^2 + (k +1)x - k = 0 ma tylko Kasia: Dla jakich wartości parametru k, równanie (k−2)x² + (k +1)x − k = 0 ma tylko ujemne rozwiązania. ćwiczenia ze wzorów Viete'a : zbiór zadań A.Kiełbasa: Proszę o wskazówki bądź poprawę błędów Ad 259 więc tak: Δ<0 a<0 Δ=(k+1)² + 4k(k −2) z Δ otrzymuję przedział k∊ ( ¹₅; 1) z a<0 k<2 k ∊( −∞; 2) rozw: k∊(− ∞; ¹₅) ∪ (1; 2) w podręczniku k∊ k∊(0; ¹₅>∪ <1; 2> jednak rozwiązanie zawiera również 0, w przedziale rozwiązań oraz domknięte przedziały przy ¹₅, 1,2. Czy pominęłam jakiś warunek?

Kaja: przy założeniu, że a<0 i Δ<0 równanie nie ma żadnego rozwiązania

Kaja: rozpatrz sobie warunki: 1. a≠2 i Δ>0 i t₁*t₂<0 i t₁+t₂<0 2. a≠2 i Δ=0 i t₀<0 3. k=2 (wtedy równanie będzie liniowe. zobacz jakie wtedy równanie będzie miało rozwiązanie)

Kejt: myślę, że chodziło bardziej o ujemne miejsca zerowe(?), bo powinnaś wg tytułu działu skorzystać ze wzorów Viete'a.. zatem: Δ≥0 x₁+x₂<0 x₁*x₂>0

Kejt: a no i oczywiście k>2, bo chodzi nam o dwa rozwiązania..

Kejt: wróć. k≠2

Bogdan: Jeśli x₁ < 0 i x₂ < 0 to (po sprawdzeniu przypadku dla a = 0): a ≠0 i Δ≥0 i x₁*x₂>0 i x₁ + x₂ < 0

Kasia: dzięki za pomoc po obliczeniach otrzymałam dla a= 0 k=2 z Δ mamy przedział (−∞: ¹₅> ∪ <1; ∞+) x₁ * x₂ > 0

−k
	> 0
k − 2

k> 1 mam problem z x₁ + x₂<0

k+1
	<0 / (k−2)
k−2

k+1< k−2 1< −2 sprzeczność ?

Mila: Kasiu, masz błąd w treści zadania: (k−2)x² − (k +1)x − k = 0 1) k−2=0⇔k=2 Mamy równanie: 0*x²−3x−2=0 −3x=2

	−2
x=		<0 dla k=2
	3

2) k≠2 teraz sprawdzaj.

Kasia: 1) tak x = ⁻²₃ ale szukamy wartości parametru k 2) a≠2 x₁ + x₂ < 0

k+1
	< 0 /(k−2) 2
k−2

(k−2)(k+1)<0

	−1
k=2 ∨ k= − 1 sprzeczność po podstawieniu otrzymujemy x2 =
	3

x₁ *x₂>0 k>2 dlaczego w rozwiązaniu z podręcznika jest 0

	1
k∊(0;		>∪ <1; 2>
	5

dla k=0 otrzymujemy równanie −2x² − x=0 Δ= 1

	0
x1 =
	−4

	−1
x2 =
	2

Mila: 1) k=2

	−2
to x=		<0 spełniony warunek
	3

lub 2)k≠2

	1
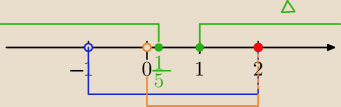
Δ≥0⇔k≤		lub k≥1 zaznaczam na osi
	5

x₁+x₂<0⇔x∊(−1,2) x₁*x₂>0⇔k*(k−2)<0⇔k∊(0,2) Część wspólna:

	1
k∊(0,		>U<1,2> ( 2 dołączone z pierwszego warunku)
	5

Mila: ?

Kasia: tak, błąd w moich obliczeniach dla x1*x2>0 rozumiem, dzięki za pomoc

Mila: