stereometria yolo: Stosunek powierzchni bocznej do powierzchni podstawy ostrosłupa prawidłowego czworokątnego jest równy k. a) Jakie wartości może przyjmowac k? b)Wyznacz cosinus kąta zawartego między sąsiednimi krawędziami bocznymi tego ostrosłupa. Oblicz miarę tego kąta dla k=√3. c) Wykaż, że cosα=−1/k2, gdzie α jest kątem między sąsiednimi ścianami bocznymi tego ostrosłupa.

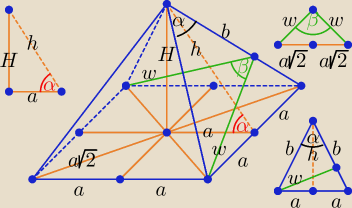
Bogdan: a)

PB		4ah		h		1		a
	= k ⇒		= k ⇒		= k ⇒		=		= cosα
PP		4a2		a		k		h

	1
α∊(0o, 90o) ⇒ (cosα)∊(0, 1) ⇒ 0 <		< 1 ⇒ k ∊ ...
	k

b)

h
	= k ⇒ h = ak, b2 = a2 + h2 ⇒ b2 = a2 + a2k2 ⇒ b2 = a2(k2 + 1)
a

Korzystając z twierdzenia kosinusów: 4a² = b² + b² − 2*b*b*cosα = 2b² − 2b²cosα = 2b²(1 − cosα) = 2a²(k² + 1)(1 − cosα) Stąd: 2 = (k² + 1)(1 − cosα) ⇒ cosα = ... c) b = a√k² + 1 , 2a*h = b*w ⇒ 2a*ak = a√k² + 1 * w ⇒ w = ... oraz w² = Z twierdzenia kosinusów otrzymujemy: 8a² = w² + w² − 2*w*w*cosβ ⇒ ... ⇒ coβ = ...