Korzystając z własności wartości bezwzględnej
Estrella:
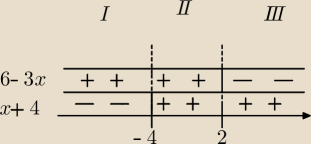
Korzystając z własności wartości bezwzględnej, wykaż, że dla
podanych wartości x prawdziwa jest równość:
3
√x2 + 8x + 16 +
√36 − 36x +9x2 = 18 , dla x∊<−4,2>
rozwiazalam metoda tzw. autostrady, czyli ide kolejno przedzialami i zmieniam znak zgodnie z
autostrada, idac od góry
I) ( −
∞ , − 4 )
3(x +4) + (− 6 + 3x ) = 18
3x +12 − 6 +3x =18
6x +6 = 18
6x = 12
x=2
∉
II) < − 4 , 2 >
3(x + 4) + 6 − 3x =18
3x + 12 +6 − 3x =18
18=18
x∊R
x∊< −4 , 2 >
czyli x∊< − 4 , 2 >
III) ( 2 , +
∞)
−3x −12 +6 −3x =18
−6x = 24
x = − 4
∉
Czy to oznacza, ze dowiodlam, ze rowność jest prawdziwa?
Prosze o sprawdzenie i z góry dziekuje.
31 gru 15:21
Estrella: sprawdzi mi ktos?
31 gru 15:24
morfik: Pięknie to zrobiłaś. Wykazałaś, że rozwiązaniem równania jest każda liczba z przedziału <−2,4>.
31 gru 15:32
5-latek: Korzystajac z wlasnosci wartosci bezwzglednej czyli takiej
√x2=|x|
x
2+8x+16=(x+4)
2
9x
2−36x+36=(3x−6)
2
3
√(x+4)2+
√(3x−6)2=3|x+4|+|3x−6|= masz przedzial opusc wiec moduky i sprawdz czy to =18
A ty popatrz co zrobilas −− jaki wyznaczylas 1 i 3 przedzial skoro przedzial masz podany ?

31 gru 15:32
morfik: oczywiście <−4,2>
31 gru 15:33
Estrella: czyli mam dobrze?
31 gru 15:53
Estrella: no tak, wiem, ale po prostu dowiodlam moim zdaniem, ze liczby naleza tylko do podaneo
przedzialu
31 gru 15:55
Estrella: tak mi sie wydaje ...
31 gru 15:55
Estrella: ?
31 gru 16:03
Aga1.: I.
3(−x−4)+6−3x=18
II dobrze
w III
3(x+4)+3x−6=18
31 gru 16:13
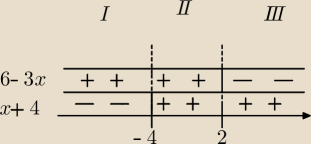 Korzystając z własności wartości bezwzględnej, wykaż, że dla
podanych wartości x prawdziwa jest równość:
3√x2 + 8x + 16 + √36 − 36x +9x2 = 18 , dla x∊<−4,2>
rozwiazalam metoda tzw. autostrady, czyli ide kolejno przedzialami i zmieniam znak zgodnie z
autostrada, idac od góry
I) ( − ∞ , − 4 )
3(x +4) + (− 6 + 3x ) = 18
3x +12 − 6 +3x =18
6x +6 = 18
6x = 12
x=2
∉
II) < − 4 , 2 >
3(x + 4) + 6 − 3x =18
3x + 12 +6 − 3x =18
18=18
x∊R x∊< −4 , 2 >
czyli x∊< − 4 , 2 >
III) ( 2 , + ∞)
−3x −12 +6 −3x =18
−6x = 24
x = − 4
∉
Czy to oznacza, ze dowiodlam, ze rowność jest prawdziwa?
Prosze o sprawdzenie i z góry dziekuje.
Korzystając z własności wartości bezwzględnej, wykaż, że dla
podanych wartości x prawdziwa jest równość:
3√x2 + 8x + 16 + √36 − 36x +9x2 = 18 , dla x∊<−4,2>
rozwiazalam metoda tzw. autostrady, czyli ide kolejno przedzialami i zmieniam znak zgodnie z
autostrada, idac od góry
I) ( − ∞ , − 4 )
3(x +4) + (− 6 + 3x ) = 18
3x +12 − 6 +3x =18
6x +6 = 18
6x = 12
x=2
∉
II) < − 4 , 2 >
3(x + 4) + 6 − 3x =18
3x + 12 +6 − 3x =18
18=18
x∊R x∊< −4 , 2 >
czyli x∊< − 4 , 2 >
III) ( 2 , + ∞)
−3x −12 +6 −3x =18
−6x = 24
x = − 4
∉
Czy to oznacza, ze dowiodlam, ze rowność jest prawdziwa?
Prosze o sprawdzenie i z góry dziekuje.
